За умовою задачі в Δ АВС сторона АВ = 14 см, ВС = 10 см, АС = 16 см.
Так як М за умовою середина АВ, то АМ = МВ = АВ : 2 = 14 : 2 = 7 (см)
Так як точка К за умовою середина АС, то АК = КС = АС : 2 = 16 : 2 = 8 (см)
Так як точка М – середина АВ і точка К – середина АВ, то відрізок МК – середня лінія трикутника.
Середня лінія трикутника паралельна третій стороні і дорівнює її половині (властивість середньої лінії трикутника). Значить МК = ВС : 2 = 10 : 2 = 5 (см)
Знайдемо периметр трикутника АМК:
Р = АМ + АК + МК = 7 + 8 + 5 = 20 (см)
Відповідь: 20 см
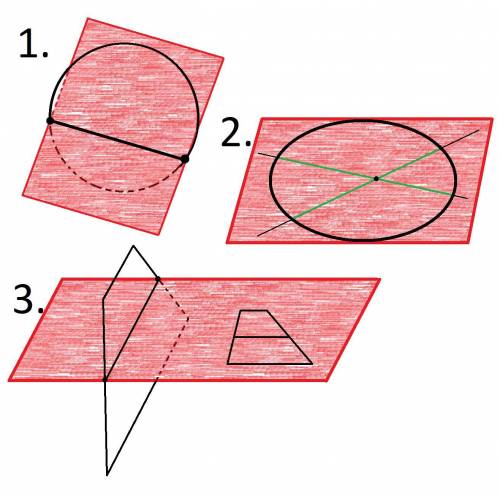
1.
Нет, неверно.
Окружность не всегда, но может пересекать эту плоскость.
2.
Да, верно.
Окружность лежит в данной плоскости т.к. две пересекающие прямые (содержащие хорды, которые пересекаются), принадлежащие плоскости окружности, содержатся в данной плоскости. А значит любая точка окружности так же принадлежит данной плоскости.
3.
Нет, не пересекает.
Средняя линия параллельна основаниям. Поэтому основания либо параллельно данной плоскости (по признаку параллельности прямой и плоскости), либо лежит в этой плоскости (ведь для параллельных прямых существует плоскость, в которой они лежат). Среди возможны взаимных расположений прямой и плоскости нету такого, что прямая будет пересекать плоскость.
48см
Объяснение:
Дано
Прямоугольный треугольник
c=50см гипотенуза
b=14см катет
а=? катет
Решение
Теорема Пифагора
а=√(с²-b²)=√(50²-14²)=√(2500-196)=√2304=
=48см