Объяснение:
1. 2, 3
1) ∠PBK и ∠MBL-смежные.
Нет, они вертикальные
2) ∠PBL и ∠MBK-вертикальнвые.
Да, они верикальные, т.к. продолжение сторон одного угла является стороной другого
3) ∠MBK-острый угол.
Да, ∠PBL=∠MBK=72°
72°<90°
4) ∠MBL-прямой угол.
Нет, ∠PBL и ∠MBL-смежные
∠MBL=180°-72°=108°
108°>90°, угол тупой
2. 52°
MA-биссектриса угла, следовательно, она делит угол на две равные части:
∠KMA=∠AML=104°/2=52°
3. ∠DCE=124°
∠DCE и ∠FCE смежные=>∠DCE=180°-56°=124°
4. DC=7см; CF=14см
FD=DC+CF
FD=DC+CF
DC-x
CF-2x
x+2x=21
3x=21
x=7
DC=7 см
CF=14 см
5. ∠NMK=48°
∠KMN=∠OMN-∠OMK=78-30=48°
Объяснение:
Дано:
Окружность с центром в точке О;
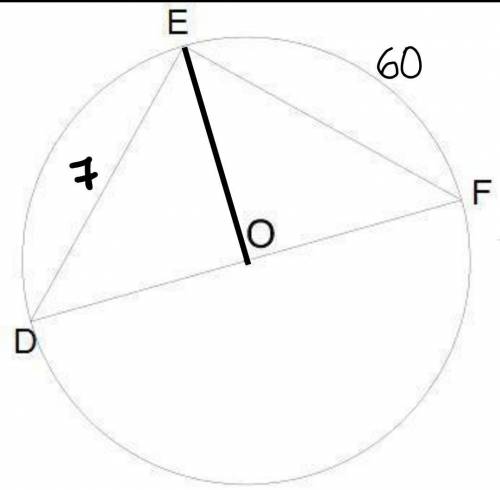
Дуга ED=60°;
ED=7 см.
Найти: длину окружности.
Проведем ЕО.
Угол ЕОF – центральный и опирается на дугу EF, тогда угол EOF=дуга EF=60°.
Угол DOE=180°–угол EOF=180°–60°=120° (смежные углы)
DO=EO так как радиусы равны, следовательно ∆ЕОD – равнобедренный с основанием ED.
Углы при основании равнобедренного треугольника равны, тогда угол DEO=угол ODE=(180°–угол DOE)÷2=(180°–120°)÷2=60°÷2=30°.
По теореме синусов в ∆EOD:
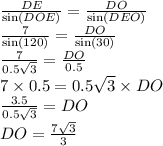
DO – радиус окружности.
C=2πr, где С – длина окружности; r – радиус окружности.
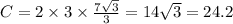
ответ: 24,2 см.
точку на ребре обозначим Р (SP / PC = 2/3)
SP = 10, PC = 15
PB1 || SB, PA1 || SA, B1A1 || BA
треугольники PA1C и SAC подобны => PC / SC = PA1 / SA = A1C / AC
3/5 = PA1 / 25
PA1 = 15 (или иначе: треугольник SAC равнобедренный => и PA1C тоже равнобедренный, т.к. они подобны => PA1 = PC = 15)
3/5 = A1C / 40 => A1C = 24 = B1C
треугольники ABC и A1B1C подобны => CA1 / CA = A1B1 / AB
24/40 = A1B1 / 40
A1B1 = 24 (или иначе: треугольник ABC равносторонний => и A1B1C тоже равносторонний, т.к. они подобны => A1B1 = CA1 = 24)
по формуле Герона Sсечения = корень(27*3*12*12) = 12*9 = 108
можно найти высоту сечения...
по т.Пифагора высота = корень(15*15 - 12*12) = корень((15-12)*(15+12)) =
корень(3*27) = 9
Sсечения = 24*9/2 = 12*9 = 108