
В кубе ABCDA₁B₁C₁D₁ диагонали грани A₁B₁C₁D₁ пересекаются в точке O. Назовите линейный угол двугранного угла DA₁C₁D₁
––––––––––––––––––––––
Определение: Двугранный угол — пространственная геометрическая фигура, образованная двумя полуплоскостями, исходящими из одной прямой, а также часть пространства, ограниченная этими полуплоскостями.
Линейный угол-это угол образованный пересечением двугранного угла с плоскостью, перпендикулярной к его ребру.
Все грани куба - квадраты. Их диагонали равны, пересекаются под прямым углом и точкой пересечения делятся пополам.
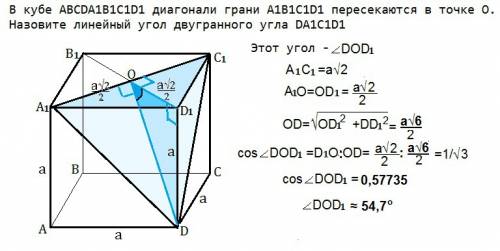
Искомый угол - это угол DOD₁ между плоскостями А₁С₁D₁ и A₁C₁D, где D₁O ⊥ A₁C₁, как половина диагонали грани, а DО ⊥ А₁С₁ как наклонная, чья проекция перпендикулярна прямой ( т. о трех перпендикулярах). Плоскость DD₁O перпендикулярна граням двугранного угла.
В приложении с рисунком найдена и примерная величина этого угла ≈ 54,7°
Мы можем провести две высоты ВК и СН ...т.к меньшее основание ВС=8см...следовательно КН=ВС=ВК=СD=8 см...Находим угодл АВК...Т.к. угол ВКА=90 градусам следовательно АВК равно 30 градусам. Т.к. В теругольнике 180 градусов мы можем вычислить ВАК=180-(30=90)=60 градусов...и теперь через синус мы можем найти АВ. sin угла А=корень из 3 делённое на 2. Теперь можем сделать соотношение.Получается Корень из 3 делённое на два= 8 делённое на АВ. АВ= 8*2/корень из 3=16/корень из 3. АВ=СD=16/на корень из 3. Периметр= 16+16+8+848