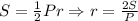
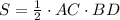
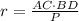
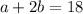Треугольник авс равнобедренный с основанием ас. определите урол 2, если угол 1 равен 56 градусам

👇

Увидеть ответ

Ответ:

Влад1111111111111121

22.04.2022

62 или 68

Объяснение:

Общая сумма всех углов треугольника равна 180⁰. Если треугольник равнобедренный и:

*известен боковой угол, то из 180⁰ вычитаем 2 таких угла и получаем вершинный угол.

*известен вершинный угол, то из 180⁰ отнимаем вершинный угол и полученное число делим на 2. Получается боковой угол равнобедренного треугольника.

В твоём случае если угол 1 является боковым, то 180⁰-2*56⁰=68⁰, если же вершинным, то (180⁰-56⁰)÷2=62⁰. Если бы ты уточнила, то ответ был бы покороче

4,5(59 оценок)

Открыть все ответы

Ответ:

oljkejik

22.04.2022

Площадь треугольника равна половине произведение его периметра на радиус вписанной окружности:
$S= \frac{1}{2} Pr\Rightarrow r= \frac{2S}{P}$

С другой стороны площадь можно найти как половина произведения основания на высоту:
$S= \frac{1}{2} \cdot AC\cdot BD$
Тогда выражение для радиуса вписанной окружности примет вид:
$r= \frac{AC\cdot BD}{P}$

Основание АС нам неизвестно, поэтому введем обозначения: AC=a, AB=BC=b, и составим систему уравнений:
Первое уравнение: a+2b=18

- периметр треугольника.
В качестве второго уравнения рассмотрим теорему Пифагора для прямоугольного треугольника BCD, где DC=а/2, так как BD - высота равнобедренного треугольника, а следовательно, и медиана.
Второе уравнение: $( \frac{a}{2} )^2+3^2=b^2$
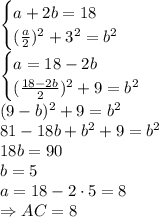
$\begin{cases} a+2b=18 \\ ( \frac{a}{2} )^2+3^2=b^2\right \end{cases}
\\\
\begin{cases} a=18-2b \\ ( \frac{18-2b}{2} )^2+9=b^2\right \end{cases}
\\\
( 9-b)^2+9=b^2
\\\
81-18b+b^2+9=b^2
\\\
18b=90
\\\
b=5
\\
a=18-2\cdot5=8
\\\
\Rightarrow AC=8$

Подставляем числовые данные в выражения для радиуса:
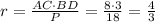
$r= \frac{AC\cdot BD}{P}= \frac{8\cdot3}{18} = \frac{4}{3}$

ответ: 4/3

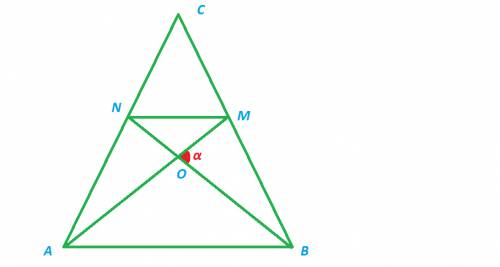
Дано: δabc, ab=bc, bd⊥ac, pδ=18, bd=3 найти: r (радиус вписанной окружности) решение:

Дано: δabc, ab=bc, bd⊥ac, pδ=18, bd=3 найти: r (радиус вписанной окружности) решение:

4,5(53 оценок)

Ответ:

Dufrenb

22.04.2022

рассмотрим прямоугольный треугольник ABC в которм угол А - прямой, угол В = 30 градусам а угол С = 60.

Приложим к треугольнику АВС равный ему треугольник АВD. Получим треугольник BCD в котором B = D = 60 градусов, следовательно DC = BC. Но по построению АС 1/2 ВС, ч т д

Если катет прямоугольного треугольника равен половине гипотенузы, то угол, лежащий против этого катета равен 30 градусам.

рассмотрим прямоугольный треугольник АВC, у которого катет АС равен половине гипотенузы АС.

Приложим к треугольнику АВС равный ему треугольник ABD. Получит равносторонний треугольник BCD. Углы равностороннего треугольника равны друг другу, поэтому каждый из них = 60 градусам. Но угол DBC = 2 угла ABC, следовательно угол АВС = 30 градусов,ч т д

4,4(62 оценок)

Это интересно:

Компьютеры-и-электроника

11.08.2021

Как настроить iPod Touch: подробное руководство...

Компьютеры-и-электроника

06.03.2022

Как сбросить пароль учетной записи на Instagram: мастер-класс с шаг за шагом инструкцией...

Кулинария-и-гостеприимство

06.06.2022

Как приготовить конфеты из сахара...

10.01.2022