
20°
Объяснение:
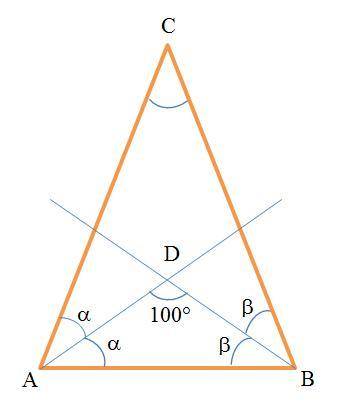
Дано (см. рисунок):
ΔАВС - равнобедренный
AD - биссектриса угла А
BD - биссектриса угла В
∠ADB = 100°
Найти: ∠С
Решение.
Так как треугольник ABC равнобедренный, то у него углы при основании равны ∠А=∠В. Биссектриса делит угол пополам, поэтому α=∠А/2 и β=∠В/2. Но ∠А=∠В и поэтому α=β. Значит, треугольник ADB также равнобедренный.
Найдём углы α и β. Сумма внутренних углов треугольника равна 180°: α + β + 100° = 180°. В силу этого α = β = (180-100)/2 = 40°.
Тогда ∠CАВ=∠СВА=2·α=2·40°=80°. Опять используем свойство:
Сумма внутренних углов треугольника равна 180°.
В силу этого ∠CАВ+∠СВА+∠С=180°. Отсюда
∠C=180°-(∠CАВ+∠СВА)=180°-(80°+80°)=180°-160°=20°.
ответ: 20°
хорда a=5√2 окружности стягивает дугу в 90 градусов - это значит, центральный угол , который опирается на эту дугу(хорду) равен 90 град
тогда отрезки (хорда +радиус+радиус) образуют прямоугольный равнобедренный треугольник с углом при вершине <O= 90 град ., здесь хорда-основание, радиусы - боковые стороны, углы при основании равны между собой <A=<B= (180-<O) /2 =(180-90) /2 =45град -тогда радиус окружности R =a/√2 = 5√2 /√2= 5
полный круг/окружность - это 360 град , тогда
длина дуги 90 град - 1/4 окружности 1/4*2п*R =п/2 *5 =5п/2
площадь сектора 90 град - 1/4 площади круга 1/4*пR^2=п/4 *25=25п/4
6. ∆АВС- прямоугольные (<С=90).
<В=90°-<А=90-60=30°(по свойству острых углов в прямоугольном треугольнике) ==> по свойству катет, лежащий против угла в 30 градусов, равен половине гипотенузы ==>АС=½АВ==>АВ=2АС=2*4=8 (см)
ответ: АВ=8 см
7. по свойству высоты, проведенной в прямоугольном треугольнике из вершины прямого угла: СД=½АВ==> АВ=2СД=2*6=12 см
ответ: 12 см.
8. х- 1 часть
<А=2х <В=х
сумма А и В=90°
составим и решим уравнение:
2х+х=90
3х=90
х=30
<А=60° <В=30°==> по свойству: катет лежащий против угла в 30 градусов равен половине гипотенузы: ==>АС=½АВ=7 см
ответ: 7 см