Дано: шар с центром в точке
R=13- радиус шара
плоскость а -сечение шара
р(а, О)=5 (расстояние от центра шара О до плоскости а
Найти: r-радиус круга в сечении
Решение
Сечением будет круг. Найдем его радиус. От центра шара до центра сечения 5 - это катет треугольника, который получится, если соединим центр шара, центр сечения и точку пересечения шара с его сечением. 13 - гипотенуза, по теорПифагора:r=√13²-5²=√144=12. S=πr²=π144=144πкв.ед
ответ: 108√3 см²
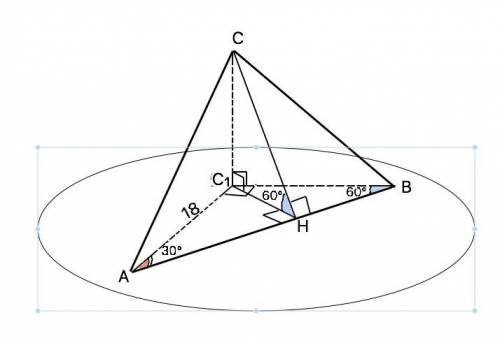
Объяснение: Угол между плоскостями данных треугольников – двугранный. Его величина определяется градусной мерой линейного угла, сторонами которого являются лучи, проведённые в его гранях перпендикулярно ребру с общим началом на нём. На приложенном рисунке СН - наклонная, С1Н - ее проекция, оба отрезка по т. о 3-х перпендикулярах перпендикулярны АВ в одной точке и составляют между плоскостями треугольников ∠СНС1=60°.
Сумма двух углов ∆ АВС1 ∠А+∠В=30°+60°=90°. Из суммы углов треугольника третий ∠С1=180°-90°=90°. ⇒ ∆ АВС1 - прямоугольный. АВ=АС1:sin60°=18:(√3/2)=12√3 см
Из ∆ АНС1 отрезок С1Н=АС1•sin∠HAC1=18•1/2=9 см
Высота СН ∆ АВС равна С1Н:cos∠CHC1=9:1/2=18 см
Ѕ(АВС)=СН•АВ:2=18•12√3:2=108√3 см²
104 см²
Объяснение:
Дано: КМРТ - трапеция, МК⊥КТ, МК=8 см, РТ=10 см. МТ - биссектриса. Найти S(КМРТ).
∠КТМ=∠РТМ по определению биссектрисы
∠РМТ=∠МТК как внутренние накрест лежащие при МР║КТ и секущей МТ, значит ΔМРТ - равнобедренный, МР=РТ=10 см.
Проведем высоту РН=МК=8 см.
КН=МР=10 см.
ΔРТН - прямоугольный, РТ=10 см, РН=8 см, значит ТН=6 см (египетский треугольник).
КТ=КН+ТН=10+6=16 см.
S=(МР+КТ):2*РН=(10+16):2*8=104 см²