Пусть МА=10см - расстояние от данной точки до плоскости. МВ наклонная, АВ - проекция, угол МВА = 30⁰, МС - наклонная, АС - проекция, угол МСА=45⁰.
Угол ВАС=30⁰. Необходимо найти ВС.
Поскольку треугольник АМС - равнобедренный, прямоугольный, то МА=АС=10см
В треугольнике АВМ(прямоугольный треугольник) найдем АВ:
АВ=АМ/tg30⁰=10/(√3/3)=10√3
Из треугольника Авс по т. косинусов найдем ВС:
ВС²=АВ²+АС²-2·АВ·АС·соs30⁰=(10√3)²+10²-2·10√3·10·√3/2=300+100-300=100
ВС=√100=10см
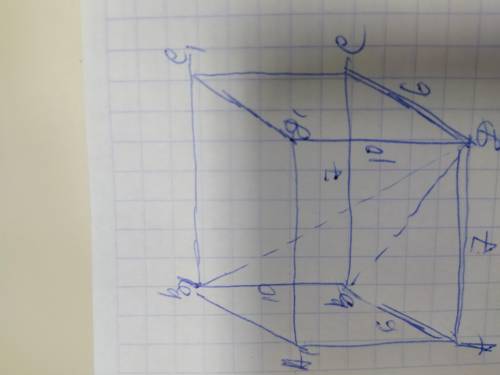
Объяснение: квадрат диагонали параллелепипеда равен сумме квадратов его измерений:
Д²=дл²+шир²+выс²=
Д²=7²+6²+10²=49+36+100=185;
Д=√185см
Если нужно найти диагонали граней параллелепипеда, тогда обозначим его вершины А В С Д В1 С1 Д1. Диагональ ВД делит грань АВСД на 2 равных прямоугольных треугольника, в которых стороны основания являются катетами а диагональ гипотенузой. Найдём диагональ ВД грани АВСД по теореме Пифагора: ВД²=АВ²+АД²=6²+7²=36+49=
=85; ВД=√85см. Такая же величина диагонали у грани А1В1С1Д1. Теперь найдём диагональ грани АА1ВВ1 также по теореме Пифагора:
АВ1²=АВ²+АА1²=6²+10²=36+100=136;
АВ1=√136=2√34см. Такая же величина диагонали у грани Д1ДС1С. Диагонали одной грани равны между собой.
Диагональ грани АА1ДД1=АД²+ДД1²=
=7²+10²=49+100=149; ДД1=√149см
Диагональ ДД1=√149см

Проекции наклонных легко вычисляются. У той наклонной, которая составляет угол в 30 градусов с плоскостью, длина проекции 10*корень(3), у второй - 10.
Даны две стороны треугольника с этими длинами, угол между ними 30 градусов, надо найти третью сторону (пусть это x). По теореме косинусов
x^2 = 10^2 + (10*корень(3))^2 - 2*10*10*корень(3)*(корень(3)/2) = 100+300-300 = 100;
x = 10;