В треугольнике ABC, периметр которого равен 20 см ,вписан круг. Отрезок касательной проведенной к окружности параллельно стороне AC, размещенной между сторонами треугольника, равен 2,4 см. Найдите сторону AC.
Объяснение:
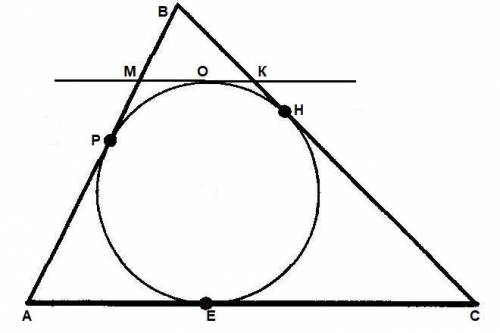
Пусть отрезок касательной проведенной к окружности параллельно стороне AC будет МК , МК=2,4 см.
Пусть точки касания располагаются так :
А-Р-В ,А-Е-С , В-Н-С , М-О-К.
ΔВМК подобен ΔВАС по двум углам : ∠ВМК=∠ВАС как соответственные и ∠В- общий.
Поэтому Р(МВК):Р(АВС)=к=МК:АС.
Выразим 1)Р(МВК), 2)АС используя свойство отрезков касательных.
1)Р(МВК)=2,4+МВ+ВК=
=2,4+(ВР-МР)+(ВН-КН)=
=2,4+(ВР-МО)+(ВН-КО)=
=2,4+(ВР+ВН)-(МО+КО)=
=2,4 +2ВР-2,4=2ВР.
Значит Р(МВК) =2ВР.
2)Р(АВС)=АВ+ВС+АС=
=(ВР+РА)+(ВН+НС)+АС=
=(ВР+АЕ)+(ВН+ЕС)+АС=
=(ВР+ВН)+(АЕ+ЕС)+АС=
=2ВР+2АС,
20=2ВР+2АС, 10=ВР+АС, ВР=10-АС.
Т.о Р(МВК):Р(АВС)=МК:АС ,
2ВР:20=2,4:АС,
АС*ВР=24 ( но ВР=10-АС), пусть АС=в ,
в(10-в)=24,
в²-10в+24=0, D=4 , в₁=4, в₂=6
АС=4см, Ас=6 см
ВС^2=AB^2+AC^2 - 2*AB*AC*cosA=11^2+8^2 - 2*11*8*cos60=121+64-2*88*1/2=97
BC=√97 см
б)
AC^2=AB^2+BC^2 - 2*AB*BC*cosB=13^2+7^2-2*13*7*cos60=169+49-2*13*7*1/2=127
АС=√127 см
2
теорема косинусов
а)
cos120= - cos60
NP^2=MN^2+MP^2 -2 MN*MP*cos120=7^2+15^2-2*7*15*(-cos60)=
=49+225-2*7*15*(-1/2)=379
NP=√379 см
б)
NP^2=
3
cos120= - cos60
а) меньшую диагональ (ВD)
лежит напротив острого угла <60
BD^2=6^2+8^2-2*6*8*cos60=36+64-2*48*(1/2)=52
BD=√52=2√13 см
б) большую диагональ (АС)
лежит напротив тупого угла <120
AC^2=6^2+8^2-2*6*8*cos120=36+64-2*48*(-1/2)=148
AC=√148=2√37 см
4
а) его стороны равны 8 мм и 10 мм, а одна из диагоналей равна 14 мм;
14^2=8^2+10^2 -2*8*10*cos<A
196=64+100 - 160*cos<A
32= - 160*cos<A
cos<A= - 32/160 =-1/5= -0.2
б) его стороны равны 12 дм и 14 дм, а одна из диагоналей равна 20 дм.
20^2=12^2+14^2 -2*12*14*cos<B
400=144+196-336* cos<B
60 =-336* cos<B
cos<B = - 60/336 = - 5/28
5
диагональ (d)и две стороны (a) (b) образуют треугольник
значит третий угол треугольника <A=180-20-60=100 град
дальше по теореме синусов
a/sin20=b/sin60=d/sinA=25/sin100
a=sin20*25/sin100=0.3420*25/0.9848=8.7 см
b= sin60*25/sin100=√3/2*25/0.9848=22 см
6
угол <С=180-<A-<B=180-30-40=110
по теореме синусов
AC/sin<B=BC/sin<A=AB/sin<C=2R
AC/sin40=BC/sin30=16/sin110
AC=sin40*16/sin110= 0.6428 *16/0.9397=10.94 см =11 см
BC= sin30*16/sin110=1/2*16/0.9397= 8.5 см
радиус описанной окружности
AB/sin<C=2R
R= AB/(2*sin<C)=16 / (2*sin110)=8/ sin110 = 8.5 см
7
8
углы параллелограмма А и В - односторонние
<A - напротив диагонали d1
<B=180-<A - напротив диагонали d2
cosA= - cosB=
d1^2=a^2+b^2-2ab*cosA
d2^2= a^2+b^2-2ab*cosB = a^2+b^2-2ab*(-cosA)= a^2+b^2+2ab*cosA
d1^2+d2^2 = a^2+b^2-2ab*cosA + a^2+b^2 +2ab*cosA = a^2+b^2 + a^2+b^2 = 2 *( a^2+b^2 )
ДОКАЗАНО сумма квадратов диагоналей равна сумме квадратов (ЧЕТЫРЕХ)сторон
9
10
11
12
13
Вроде это, Заранее незочто