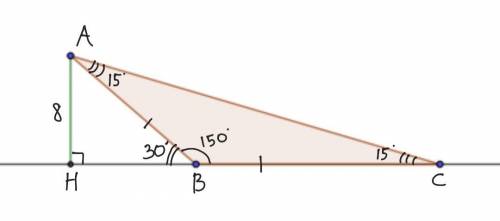
Дано: ΔABC - равнобедренный, АС - основание, АВ=ВС, ∠В=150°, АН - высота, АН = 8 е.д.
Найти: BC.
Решение.
Поскольку треугольник тупоугольный, а высота проведена из острого угла, то высота принадлежит продолжению противолежащей стороны.
Поэтому рисуем продолжение прямой ВС и высоту АН, проведённую к нему.
В ΔАНВ: ∠НВА = 180°-150°= 30° (как смежные).
АНВ - прямоугольный треугольник (АН ведь высота) с гипотенузой АВ.
В прямоугольном треугольнике, если острый угол равен 30°, то противолежащий этому углу катет равен половине гипотенузы.
АН=½АВ.
АВ= 2АН.
АН по условию 8, тогда АВ= 2×8=16.
ΔАВС - равнобедренный, АВ=ВС. Значит, ВС=16 е.д.
ответ: 16 е.д.
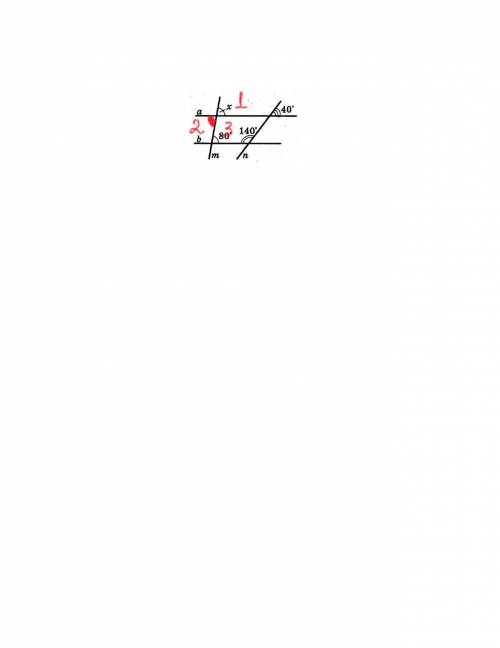
Объяснение:
Итак, когда секущая пересекает параллельные прямые, образуется несколько видов углов:
1) Внутренние накрест лежащие (которые равны)
2) Внутренние односторонние углы(их сумма составляет 180 градусов)
3) Соответственные углы(они равны)
Я отметил на рисунке угол x как угол 1.
Угол 1 будет равен углу 2, т.к. они вертикальные, а это значит, что угол 2 будет равняться x.
А угол 3(который имеет градусную меру в 80 градусов) будет равен углу 2, так как они накрест лежащие. А это значит, что угол x будет равен 80 градусов.
Задача решена.
В правильной 4-хугольной пирамиде основанием является квадрат, а высота
пирамиды проектируется в центр основания. Боковое реброобразует с плоскостью
основания угол 45 градусов, значит высота пирамиды будет равна половине
диагонали основания и будет равна 2 см. А площадь основания (квадрата)
будет равна половине произведения его диагоналей S осн = 1/2*4*4 = 8(см^2)
V пир = 1/3Sосн*H
Vпир = 1/3 * 8*2 = 16/3 = 5целых 1/3(см^3)