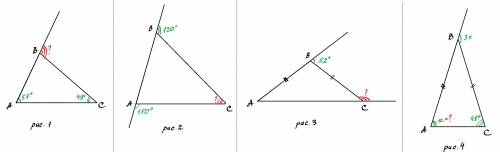
1) См. рис. 1.
В треугольнике внешний угол равен сумме двух внутренних углов не смежных с ним.
Внешний угол при вершине В равен сумме угла А и угла С.
57°+49° = 106°.
ответ: 106°.
2) См. рис. 2.
∠ВАС = 180°-150° = 30°
∠АВС = 180°-120° = 50°
∠С = 180°-∠ВАС-∠АВС = 180°-30°-50°=90°
ответ: ∠С = 90°.
3) См. рис. 3.
∠АВС = 180°-52° = 128°.
∠ВАС = ∠ВСА = (180°-128°):2 = 52°:2 = 26°.
Внешний угол при вершине основания равен 180°-26° = 154°.
Овтет: 154°.
4) См. рис. 4.
Пусть ∠А = х, тогда внешний угол при вершине В равен 3х.
Внешний угол треугольника равен сумме двух внутренних углов не смежных с ним. Значит, 3х = х+48°.
2х=48°
х=24°
ответ: ∠А = 24°.
Дано: AC=20 см
угол ABC = 120°
Найти: BH.
1) треугольник ABC - равнобедренный (по условию), отсюда следует, что углы BAC и BCA равны и каждый из них по 30° ((180-120)/2).
2) т.к. высота в равнобедренной треугольнике является и медианой, и бессектрисой, то отсюда следует: угол ABH = 60°
AH=HC=10 см
треугольник ABH - прямоугольный( BH - высота).
3) Рассмотрим треугольник ABH:
Угол ABH = 60°
AH=10 см.
Раз SIN угла в прямоугольном треугольнике - это отношения противолежащего катета к гипотенузе, то составим пропорцию:
SIN60°=AH/AB
√3/2=10/AB
AB=10/(√3/2)
AB=20/√3
4) По теореме Пифагора находим BH:
AB²=BH²+AH²
1200=BH²+100
BH²=1200-100
BH²=1100
BH=√1100
BH=10√11
ответ: BH = 10√11. Надеюсь, верно)
В: 12см
Объяснение:
Дано
P = 12см
Знайти
d-?
Розв'язок
d= P/2√2
d= 12√2/2√2
= 12cм