Сумма острых углов прямоугольного треугольника 90°⇒
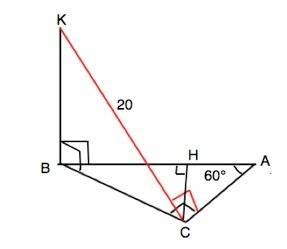
∠АВС=90°-60°=30°
∆ ВСН прямоугольный, СН противолежит углу 30°.По свойству прямоугольного треугольника с углом 30° гипотенуза ВС = 2•СН=16 см
Расстояние от точки до прямой - длина отрезка, проведенного перпендикулярно к ней.
ВС⊥АС, ВС - проекция КС.
По т. о 3-х перпендикулярах КС⊥АС.⇒ КС - данное в условии расстояние от К до АС.
По условию ВК перпендикулярна плоскости АВС, следовательно, перпендикулярна любой прямой, проходящей через В. ⇒
∆ КВС прямоугольный,
По т.Пифагора КВ=√(KC²-BC²)=√(400-256)=12 см
* * * * * * * * * * * * * * * * * * * * * * * * * *
В равнобедренной трапеции диагональ является биссектрисой. Найдите площадь трапеции, если боковая сторона - 25 см, основание 39 см
ответ: 768 см².
Объяснение: Пусть ABCD равнобедренная трапеция
AD и BC основания трапеции ( AD || BC ) AD =39 см ,
ВA = CD =25 см и ∠ BAC = ∠ DAC .
S(ABCD) = h*(AD+BC)/2 -?
--------------------------------------
∠ BCA= ∠ DAC как накрест лежащие углы ( BC || AD , CA секущая) ,
следовательно ∠ BCA= ∠ DAC =∠ BAC , т.е. ΔBAC равнобедренный
BA = BC =25 см получили BA = CD =25 см .
Проведем BB₁ ⊥ AD и CC₁ ⊥ AD . BCC₁B₁ _прямоугольник BB₁ =CC₁
B₁C₁ = BC =25 см ; Δ BB₁A = Δ CC₁D(гипотен. BA= CD и катеты BB₁ =CC₁).
AB₁ =(AD - BC)/2 =(39 - 25)/2 см=7 см .
Из Δ BB₁A по теореме Пифагора:
BB₁ =√(BA² -AB₁² ) =√(25² -7)² =√(625 -49) =√576=24 (см) .
* * * h=√(25²-7)² =√(25 -7)(25 +7) =√(18*32) √(9*2*16*2)=3*2*4=24 * * *
S(ABCD) = h*(AD+BC)/2 =24(39+25)/2 =24*32 = 768 (см²).

Каждый шаг - это шаблонное построение циркулем и линейкой.
1. Проводится прямая, из какой-то точки А этой прямой проводится луч под заданным углом к прямой.
2. На на этом луче берется произвольная точка В и опускается перпендикуляр на прямую, его основание пусть С.
3. Проводится окружность с центром в точке В радиусом ВС. Она пересекает луч между точками А и В в точке Е.
Теперь остается построить треугольник, подобный треугольнику АВС, но чтобы отрезок, соответствующий АЕ, в этом треугольнике был бы равен заданной разности гипотенузы и катета. Для этого
4. Рядом с точкой А на прямой АС выбирается точка А1 и из неё проводится второй луч параллельно АВ.
5. От точки А1 на втором луче откладывается точка Е1, так, что А1Е1 равно заданной разности.
6. Через точки ЕЕ1 проводится прямая ЕЕ1, и через точку С - прямая, параллельная ЕЕ1, до пересечения с лучем А1Е1 в точке В1.
7. Из точки В1 на прямую АС опускается перпендикуляр, основание которого С1.
Треугольник А1В1С1 и есть нужный треугольник.