
ответ:√3/3
* * *
Косинус угла- отношение катета, прилежащего к углу, к гипотенузе.
Нужный угол равен линейному углу двугранного угла между данными плоскостями. Линейным углом двугранного угла называется угол, сторонами которого являются лучи с общим началом на ребре двугранного угла, которые проведены в его гранях перпендикулярно ребру.
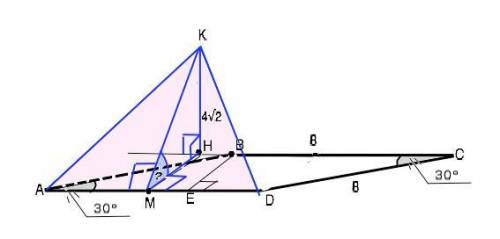
Сделаем и рассмотрим рисунок, соответствующий условию задачи. КН - расстояние от т.К до плоскости ромба. ВЕ - высота ромба. cos ∠КМН - искомый.
ВЕ⊥АD=АВ•sin30°=8•1/2=4 см.
КН⊥ВС, НМ⊥АD, НМ=ВЕ=4 см ( расстояние между параллельными прямыми равно в любой точке)
По т. о 3-х перпендикулярах КМ⊥АD. Т.к. ∆ АКD правильный, его углы равны 60°.⇒ КМ=АК•sin60°=4√3 или по т.Пифагора из ∆ КНМ получим тот же результат. ⇒ cos∠KMH=МН/КМ=4/4√3=1/√3 или иначе √3/3
228√3
Объяснение:
У равнобокой трапеции углы при основании равны, значит есть 2 пары углов по 150 и по 180-150. т.е. по 30, боковая сторона 12 корней из 3, а меньшее основание 20, но большее основание равно меньшему основанию + 2 остатка треугольника. Высота - перпендекуляр, следовательно треугольники прямоугольники. катет напротив угла в 30 градусов равен половине гипотенузы, т.е. 6 корней из трех, найдем остаточек треугольника, 12 корней из трех в квадрате минус 6 корней из трех в квадрате равно 144*3-36*3=3(144-36)=3*108=324, корень из 324 - 18, значит этот остаток треугольника 18, значит 2 остатка 36, следовательно большее основание равно 20+36=56, площадь трапеции находится по формуле полусумма оснований на высоту, тогда 56+20=76/2=38* высоту, а высота 6 корней из трех, т.е. 228√3