3.Дано следующее соотношение углов в треугольнике : А:В:С=1:2:3.
Найдите углы треугольника.
С рисунком!

Question

Геометрия: 3.Дано следующее соотношение углов в треугольнике : А:В:С=1:2:3. Найдите углы треугольника. С рисунком!

tagirova2 · Accepted Answer

Если три стороны одного треугольника соответственно пропорциональны трем сторонам другого треугольника, то такие треугольники подобны.

Дано: ΔАВС, ΔА₁В₁С₁,

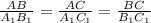
$\frac{AB}{A_{1}B_{1} } =\frac{AC}{A_{1}C_{1}}=\frac{BC}{B_{1}C_{1}}$

Доказать: ΔАВС подобен ΔА₁В₁С₁.

Доказательство:

На стороне АС треугольника АВС отложим СА₂ = С₁А₁ и проведем А₂В₂║АВ.

Так как прямая, параллельная стороне треугольника, отсекает треугольник, подобный данному, то

ΔАВС подобен ΔА₂В₂С , значит их стороны пропорциональны:

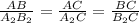$\frac{AB}{A_{2}B_{2} } =\frac{AC}{A_{2}C}=\frac{BC}{B_{2}C}$ , а так как А₂С = А₁С₁, то получаем

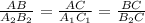$\frac{AB}{A_{2}B_{2} } =\frac{AC}{A_{1}C_{1}}=\frac{BC}{B_{2}C}$ ,

По условию:

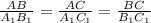$\frac{AB}{A_{1}B_{1} } =\frac{AC}{A_{1}C_{1}}=\frac{BC}{B_{1}C_{1}}$ .

Из этих двух равенств следует, что

А₂В₂ = А₁В₁ и В₂С = В₁С₁.

Тогда ΔА₁В₁С₁ = ΔА₂В₂С по трем сторонам.

Значит,

ΔАВС подобен ΔА₁В₁С₁.