См вложение.
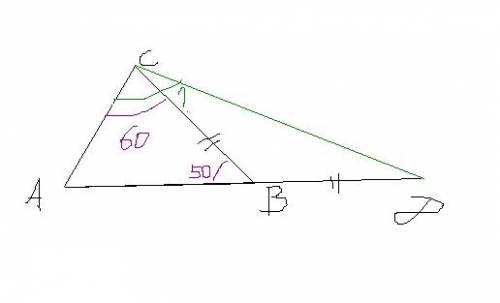
Треугольник СBD равнобедренный поэтому уголы BCD=BDC=50/2=25, то есть их сумма равна смежному при вершине.
ACD=60+25=85
66 см²
Объяснение:
Медианы треугольника пересекаются в одной точке, и точкой пересечения делятся в отношении 2:1, считая от вершины.
⇒ ВМ:МК=2:1.
У ΔАМК и ΔАВМ одна и та же высота АН - перпендикуляр, проведенный из вершины А к прямой ВК, содержащей стороны ВМ и МК этих треугольников.
Если два треугольника имеют одинаковые высоты, то отношение их площадей равно отношению длин оснований (сторон, на которые опущены эти высоты) ⇒
Samk/Sabm=1/2 ⇒
11/Sabm=1/2 =>
22=Sabm.
Sabk=22см²+11см²=33см²
медиана ВК делит ΔАВС на два равновеликих т.е Sabk = Skbc.
⇒
Sabc=33*2=66см²
Угол СВД и угол СВА смежные, угол СВД=180-50=130
Угол ВДС и угол ВСД равны т.к. треугольник ВСД является равнобедренным (ВС=СД)
Значит по теореме о сумме углов треугольника угол ВСД=угол ВДC=(180-130):2=25
Тогда угол АСД=угол АСВ+уголВСД=60+25=85.