
Объяснение:
Биссектриса угла В и биссектриса внешнего угла D прямоугольника ABCD пересекают сторону AD и прямую АВ в точках М и К соответственно. Докажите, что отрезок МК равен и перпендикулярен диагонали прямоугольника.
2. В равнобедренном треугольнике АВС на боковой стороне ВС отмечена точка М так, что отрезок СМ равен высоте треугольника, проведенной к этой стороне, а на боковой стороне АВ отмечена точка К так, что угол КМС – прямой. Найдите угол АСК.
3. Из листа бумаги в клетку вырезали квадрат 2×2. Используя только линейку без делений и не выходя за пределы квадрата, разделите диагональ квадрата на 6 равных частей.
4. В трапеции ABCD: AB = BC = CD, CH – высота. Докажите, что перпендикуляр, опущенный из Н на АС, проходит через середину BD.
5. Пусть AA1 и BB1 – высоты неравнобедренного остроугольного треугольника АВС, М – середина АВ. Окружности, описанные около треугольников AMA1 и BMB1 пересекают прямые АС и ВС в точках К и L соответственно. Докажите, что К, М и L лежат на одной прямой.
6. Один треугольник лежит внутри другого. Докажите, что хотя бы одна из двух наименьших сторон (из шести) является стороной внутреннего треугольника.
10–11 класс
1. AD и BE – высоты треугольника АВС. Оказалось, что точка C', симметричная вершине С относительно середины отрезка DE, лежит на стороне AB. Докажите, что АВ – касательная к окружности, описанной около треугольника DEC'.
2. Прямая а пересекает плоскость α. Известно, что в этой плоскости найдутся 2011 прямых, равноудаленных от а и не пересекающих a. Верно ли, что а перпендикулярна α?
3. Дана неравнобокая трапеция ABCD (AB||CD). Произвольная окружность, проходящая через точки А и В, пересекает боковые стороны трапеции в точках P и Q, а диагонали – в точках M и N. Докажите, что прямые PQ, MN и CD пересекаются в одной точке.
4. Докажите, что любой жесткий плоский треугольник T площади меньше четырёх можно просунуть сквозь треугольную дырку Q площади 3.
5. В выпуклом четырехугольнике ABCD: AC ⊥ BD, ∠BCA = 10°, ∠BDA = 20°, ∠BAC = 40°. Найдите ∠BDC. (ответ выразите в градусах.)
6. Пусть AA1, BB1 и CC1 – высоты неравнобедренного остроугольного треугольника АВС; окружности, описанные около треугольников АВС и A1B1C, вторично пересекаются в точке Р, Z – точка пересечения касательных к описанной окружности треугольника АВС, проведённых в точках А и В. Докажите, что прямые АР, ВС и ZC1 пересекаются в одной точке.
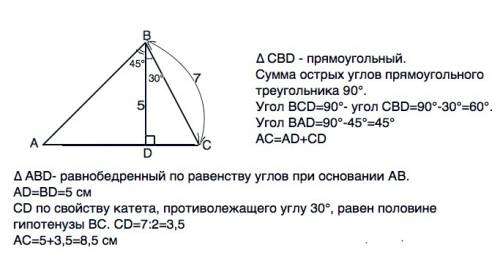
Дано: угол CDB=90°, угол ABD= 45°, угол CBD= °,. BC= 7 см, BD= 5 см. Найти: угол A, угол C, AC.
————
Сделаем по данному условию рисунок и рассмотрим прямоугольные треугольники АВD и СВD, на которые ВD разбила исходный.
Сумма острых углов прямоугольного треугольника 90°.
∠ВАD=90°- 45°=45°
⊿ АВD- равнобедренный по равенству углов при основании АВ ⇒ АD=BD=5 см
∠CDB=90°и угол СВD=30°(дано),⇒ В ⊿ ВСD ∠С=90°-30°=60°.
Длина отрезка равна сумме длин составляющих его частей⇒ АС=AD+CD
Катет прямоугольного треугольника, противолежащий углу 30°, равен половине гипотенузы. ⇒ CD=1/2•BC=7:2=3,5 см, из чего следует: АС=АD+DC=5+3,5=8,5 см.
НО!
По т.Пифагора квадрат гипотенузы равен сумме квадратов катетов. ⇒ СD=√(BC²-ВD²)=√24=2√6, и не равно 3,5
Следовательно, треугольник ВСD с гипотенузой 7 и катетом 5 не может иметь острый угол 30°, если он прямоугольный.
Величина угла СВD -по ошибке или намеренно ( бывает и так), - дана неверно.
Найдем искомый угол C по его синусу.
sinC=ВD/BC=5/7=0.7142857142857143 По таблице Брадиса или по калькулятору находим его величину. ∠С=45,58° .
Тогда СD=BC•cos45,58°=7•0,6999≈4,9 см ⇒
АС=5+4,9≈9,9 см.
.
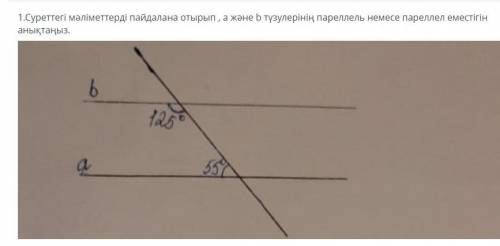
Угол 125 градусов и угол 55 градусов называются односторонними и ВСЕГДА их сумма составляет 180 градусов
125+55=180 градусов
Если при пересечении двух прямых третьей секущей сумма односторонних углов равна 180 градусов,то прямые параллельны
Номер 2
Если внешние углы треугольника равны между собой,то равны и смежные им внутренние углы,а это обозначает,что треугольник равнобедренный,если одна из сторон равна 6 см,и это основание треугольника,а периметр равен 64 см,то каждая боковая сторона,а они в равнобедренном треугольнике равны между собой,равна
(64-6):2=29 сантиметров
Номер 3
Внешний и смежный ему внутренний угол в сумме равны 180 градусов
<А=180-120=60 градусов
Так как треугольник прямоугольный,то <В=180-(90+60)=30 градусов
Значит,АС+АВ=21 см ,где
АВ-гипотенуза
АС-катет,который расположен против угла 30 градусов
По определению,катет,лежащий против угла 30 градусов вдвое меньше гипотенузы
Катет-Х
Гипотенуза-2Х
Х+2Х=21
ЗХ=21
Х=21:3
Х=7
АС=7 см
АВ=7•2=14 см
Объяснение: