Даны кривая у = х - х^3 и прямая у = 5х
.
Находим их общую точку - точку пересечения.
Приравняем х - х^3 = 5х,
4x + х^3 = 0,
x(4 + x^2) = 0,
x = 0 один корень,
x^2 = -4 не имеет решения.
Угол между кривой и прямой равен углу между касательной к кривой и прямой.
Тангенс угла наклона касательной к оси Ох равен производной функции.
y' = 1 - 3x^2.
В точке х = 0 производная равна 1, то есть tg(fi) = 1.
Угол между прямыми находим по формуле:
tgα = (k2 - k1)/(1 + k2*k1) = (5 - 1)/(1 + 5*1) = 4/6 = 2/3.
α = arctg(2/3) = 0,5880 радиан или 33,690 градуса.
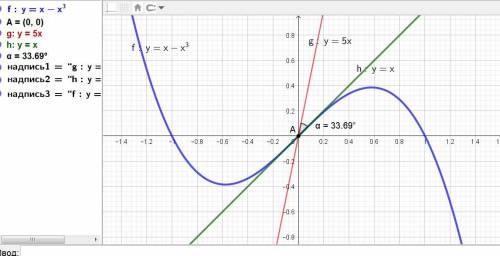
Объяснение:
1. Найдите градусную меру угла С треугольника АВС, если А = 120, В = 40.
Решение.
180°-(120°+40°)=180°-160°=20°.
***
2. В треугольнике АВС угол С прямой, А = 30, АВ = 16 см. Найдите ВС.
ВС - катет. АВ -- гипотенуза. Угол А=30°.
Катет, лежащий против угла в 30° равен 1/2 гипотенузы. ВС= 1/2 * 16 = 8 см.
***
3. В треугольнике ABC AC = BC. Внешний угол при вершине B равен 125°. Найдите угол C.
Внешний и внутренний углы - смежные их сумма равна 180°.
Угол В= 180° - 125°= 55°;
АВ - основание равнобедренного треугольника. Значит угол А равен углу В и равен 55°.
Угол при вершине (угол С) равен 180°-2*55°=180°-110°=70°.
1. Если построить ВСЕ ТРИ треугольника, образованные высотой пирамиды, апофемой и её проекцией на основание, то это будут прямоугольные треугольники с равными острыми углами, поскольку грани равнонаклонены к основанию. Поэтому равны все апофемы, и - главное - равны их проекции на основание.
То есть проекция вершины пирамиды - это точка, равноудаленная от сторон основания, то есть центр вписанной в основание окружности.
2. В плоскости этого треугольника (можно взять любой из трех, они одинаковые) лежит и отрезок от точки на высоте до стороны основания, заданный в условии, - этот отрезок соединяет эту точку с вершиной апофемы, и образуется равнобедренный треугольник, внешний угол при вершине у которого равен π/2 - β (я считаю, что угол β - это угол между этим отрезком и плоскостью основания, в условии тут неточность - если задан угол с боковой гранью, то β' <=> π/4 - β/2 ). Поэтому острые углы этого равнобедренного треугольника равны π/4 - β/2, причем один из них - это угол между апофемой и высотой пирамиды.
Поэтому радиус вписанной в основание окружности равен
r = h*tg(π/4 - β/2);
3. С другой стороны, катеты прямоугольного треугольника в основании равны
a = r*(1 + tg(α/2)); b = r*(1 + ctg(α/2));
откуда площадь основания
S = r^2*(1 + tg(α/2))*(1 + ctg(α/2))/2 = r^2*(1 + 1/sin(α)) = h^2*(1 + 1/sin(α))*(tg(π/4 - β/2))^2 = h^2*(1 + 1/sin(α))*(1 - sin(β))/(1 + sin(β));
Объем пирамиды равен
V = S*h/3 = (h^3/3)*(1 + 1/sin(α))*(1 - sin(β))/(1 + sin(β));