ответ: 8 сторон
Объяснение: Сумма внешних углов выпуклого многоугольника ( любого) равна 360°.
Сумма внутренних углов данного многоугольника по условию
360°+720°=1080°.
Если N- сумма внутренних углов, то их количество находят по формуле
N=180°•(n-2), где n - число сторон многоугольника.
1080°=180°•n -360° , откуда
n=1448°:180°=8
Иногда удобнее применять другой с тем же результатом).
Сколько бы ни было сторон у выпуклого многоугольника, каждый внутренний угол с одним внешним при той же вершине составляет в сумме 180° ( развернутый угол).
Сумма внутренних (1080°) и внешних ( 360°) углов данного многоугольника = 1080°+360°= 1440°
Делим на величину развёрнутого угла:
1440°:180°=8 ( сторон),
ответ: 8 сторон
Объяснение: Сумма внешних углов выпуклого многоугольника ( любого) равна 360°.
Сумма внутренних углов данного многоугольника по условию
360°+720°=1080°.
Если N- сумма внутренних углов, то их количество находят по формуле
N=180°•(n-2), где n - число сторон многоугольника.
1080°=180°•n -360° , откуда
n=1448°:180°=8
Иногда удобнее применять другой с тем же результатом).
Сколько бы ни было сторон у выпуклого многоугольника, каждый внутренний угол с одним внешним при той же вершине составляет в сумме 180° ( развернутый угол).
Сумма внутренних (1080°) и внешних ( 360°) углов данного многоугольника = 1080°+360°= 1440°
Делим на величину развёрнутого угла:
1440°:180°=8 ( сторон),

1) 1м.
2) 21 кв. ед.
3) 34.25 кв. ед.
Объяснение:
Дано. Стороны грядки, имеющей форму прямоугольника, равны 2,5 м и 0,4м.
Найти периметр грядки, равновеликой данной и имеющей форму квадрата.
Решение.
Равновеликие прямоугольник и квадрат у которых равные площади.
Найдем площадь прямоугольника
S=ab = 2.5 * 0.4 = 1 м².
S квадрата = S прямоугольника
S квадрата =a²; a²=1;
a=±1; (-1 - не соответствует условию.)
а=1 м.
Равновеликим прямоугольнику со сторонами 2,5 м и 0,4 м является квадрат со стороной 1 м.
***
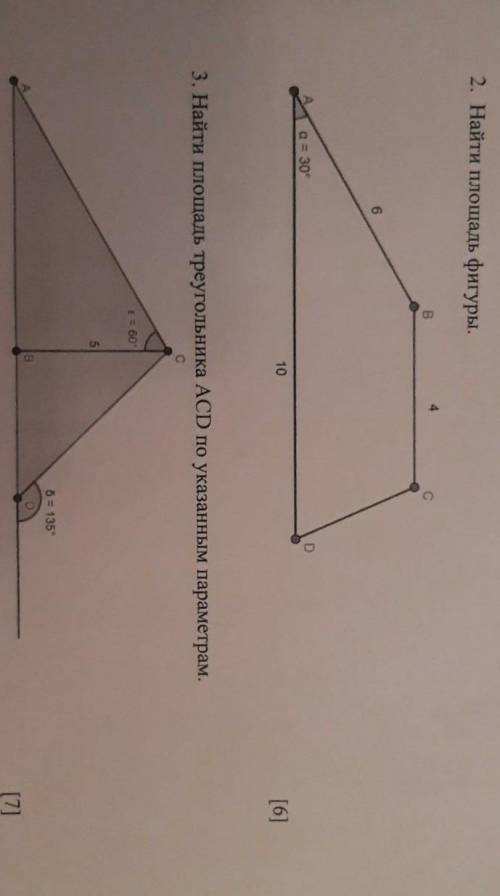
2) Дано. ABCD - трапеция. AB=6; BC=4; AD=10; угол A=30*.
Найти площадь.
Решение.
Проведем высоту ВЕ. Получили треугольник АВЕ, в котором угол А=30* АВ=6 - гипотенуза. АЕ и ВЕ - катеты, а ВЕ=h - еще и высота трапеции.
BE =h = AB* sin 30*=6*1/2=3.
Площадь S=h(a+b)/2 = 3*(10+4)/2=3*14/2=21 кв. ед.
***
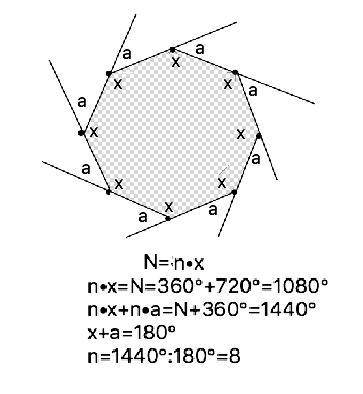
3) Дано. Δ ACD, у которого ∠А=30°; ∠ACB=60°; внешний угол D = 135°; BC=5 - высота. Найти площадь.
Решение.
В Δ BCD внутренний угол В = 180°-135° = 45°. Следовательно Δ BCD - равнобедренный ВС=BD = 5.
Из Δ АВС АВ = ВС/ tg30° = 5/0.577 = 8,7.
AD = 8,7 + 5=13,7.
Площадь S=1/2*AD*BC = 1/2* 13.7*5 = 34.25 кв. ед.