1) угол СДА вписанный, опирается на диаметр, значит он равен 90 градусов, значит треугольник АСД прямоугольный. По теореме Пифагора в^2= (4х)^2 + ( 3х)^2, откуда х=в/5.
Значит АД=4в/5, а СД=3в/5.
2) Т.к. угол СДА прямой, значит СД - высота прямоугольного треугольника АСВ, а значит, что она есть среднее геометрическое отрезков АД и ДВ, т.е. СД^2= АД*ДВ. Получаем
9в^2/25=4в/5*ДВ, откуда ДВ = 9в/20. Значит АВ = АД+ДВ= 5в/4.
3) катет СВ=4в/4 по теореме Пифагора.
4) в треугольнике ОСВ по теореме Пифагора ОВ=корень квадратный из 13 умноженный на в и деленный на 4.

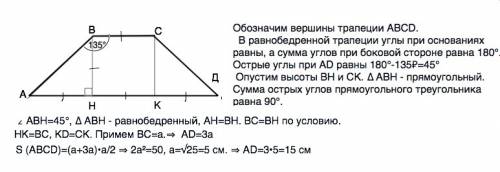
Обозначим вершины трапеции АВСD. В равнобедренной трапеции углы при основаниях равны, а сумма углов при боковой стороне равна 180°.
Острые углы при АD равны 180°-135₽=45°
Опустим высоты ВН и СК. ∆ АВН - прямоугольный. Сумма острых углов прямоугольного треугольника равна 90°.
∠ АВН=45°, ∆ АВН - равнобедренный, АН=ВН. ВС=ВН по условию. НК=ВС, КD=СК. Примем ВС=а.⇒ АD=3а
S (АВСD)=(а+3а)•a/2 ⇒ 2a²=50, a=√25=5 см. ⇒ АD=3•5=15 см
Получается треугольник АДС, вписанный в окружность с диаметром АС.
Следовательно треугольник АДС прямоугольный и в нём АС гипотенуза.
Так как в прямоугольном треугольнике АВС СД перпендикулярно гипотенузе АВ>
треугольник АВС подобен треугольнику СВД и треугольнику АСД. Из подобия треугольников следует, чт стороны у них пропорциональны.
СВ:АС = СД:АД > СВ = АС*СД/АД = в*3/4. Пусть О центр описанной окружности > АО = ОС = АС/2 = в/2
ВО = V(ВС^2 + OC^2) = V((3в/4)^2 + (в/2)^2) = V(9в^2/16 + в^2/4) = V(13в^2/16) =
= вV13/4
ответ. вV13/4