 °
° ° + 13° =
° + 13° = 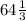 °
° °;
°;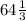 °
°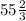 °
°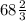 °
°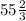 °
°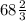 °
° 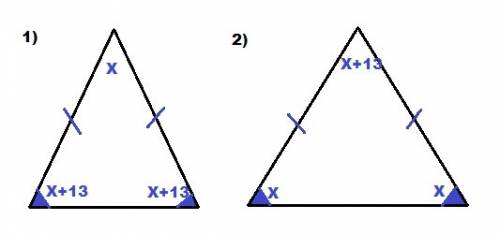
В ∆ АВС стороны АВ=ВС. Углы при основании равнобедренного треугольника равны ( свойство).
Пусть ∠АВС=α, тогда ∠ВАС=∠ВСА=2α.
Сумма углов треугольника 180°. 2α+2α+α=180° α=180°:5=36° .
Углы при основании равны 2•36°=72°.
Углы ВАМ=САМ=36°. В ∆ ВАМ углы АВМ и ВАМ равны по 36°.
∆ ВАМ - равнобедренный, ВМ=АМ.
Но угол АМС=180°-72°-36°=72°.
∆ АМС равнобедренный, и АМ=АС. ⇒. ВМ=АС.
-------
Задачу можно решать, не высчитывая величину углов.
Если угол ВАС=2α, то угол ВАМ=САМ=α , и тогда угол АМС=2α.
∆ МАС - равнобедренный, ∆ ВАМ - равнобедренный, и ВМ=АМ=АС.
Площадь полной поверхности призмы равна площади боковой поверхности + две площади оснований
Площадь боковой поверхности равна произведению периметра основания на высоту
Р=3*а=3*8=24 (см)
S=24*10=240 (см^2)
Площадь правильного треугольника
S=(a^2√3)/4=(8^2√3)/4=16√3
Площадь полной поверхности:
S=240 + 2*16√3 = 240 + 32√3 (см^2)
Объяснение: