1. Чтобы найти координаты вектора AC, нужно вычислить разности координат точек C и A:
AC = (2 - 3 ; 0 - (-1)) = (-1 ; 1)
Аналогично, чтобы найти координаты вектора BD, нужно вычислить разности координат точек D и B:
BD = (3 - 4 ; 1 - 1) = (-1 ; 0)
2. Чтобы найти вектор, равный BD - СА, нужно вычесть из координат вектора BD координаты вектора AC:
BD - СА = (-1 - (-1) ; 0 - 1) = (0 ; -1)
3. Для определения угла между векторами CA и DB используется формула скалярного произведения векторов:
cosθ = (CA · DB) / (|CA| * |DB|)
где θ - искомый угол, · - скалярное произведение, |CA| и |DB| - длины векторов CA и DB соответственно.
Длина вектора CA вычисляется по формуле |CA| = √((x2 - x1)^2 + (y2 - y1)^2), где (x1, y1) и (x2, y2) - координаты точек A и C соответственно.
Скалярное произведение CA · DB вычисляется как произведение соответствующих координат и их сумма:
CA · DB = (-1 * (-1) + 1 * 0) = 1
Теперь можно вычислить cosθ:
cosθ = 1 / (√2 * √17)
Значение cosθ можно найти в таблице косинусов или с помощью калькулятора. Пусть cosθ = 0.5, тогда θ = arccos(0.5). Найденный угол в радианах можно перевести в градусы, если нужно.
4. Заданы следующие условия:
ВМ - 6BD
AN - 4AC
Координаты точек М и N можно найти, выполнив некоторые математические операции.
VM = -6 * BD = (-6 * (-1) ; -6 * 0) = (6 ; 0)
AN = 4 * AC = (4 * (-1) ; 4 * 1) = (-4 ; 4)
Таким образом, координаты точки M равны (6 ; 0), а координаты точки N равны (-4 ; 4).
5. Чтобы выразить векторы AB и VM через векторы AB и AM, нужно использовать свойство ассоциативности суммы векторов.
AB = AM + MB
VM = AB - AM
Таким образом, чтобы выразить AB, можно воспользоваться формулой AB = AM + MB. А чтобы выразить VM, можно воспользоваться формулой VM = AB - AM.
6. Для доказательства параллелограмма ABNM нужно проверить равенство соответствующих сторон и противоположных сторон, а также равенство соответствующих углов и противоположных углов.
- Проверяем равенство сторон: AB = NM и AM = BN
- Проверяем равенство противоположных сторон: AN = MB и BM = NA
- Проверяем равенство соответствующих углов: ∠BAM = ∠BNM и ∠ABM = ∠ANM
- Проверяем равенство противоположных углов: ∠AMB = ∠ANB и ∠BMA = ∠NMA
Если все эти условия выполняются, то четырехугольник ABNM является параллелограммом.
task 43161987
АВСА₁В₁С₁-правильная призма , АВ=2√3 , МС⊥АВ, ∠С₁МС=30°. Найти площадь боковой поверхности.
Объяснение:
У правильной призмы в основании лежит равносторонний треугольник , у которого все углы по 60° . Т.к. МС⊥АВ , то ΔМСВ-прямоугольный ,
sin 60 =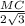
, 
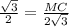, MC=3
Т.к АВСА₁В₁С₁-правильная призма , то боковые ребра перпендикулярны плоскости основания и СС₁⊥МС ⇒
ΔСС₁М прямоугольный , tg30=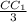
, CС₁=3√3 .
S(бок прав. призмы)=Р(осн)*h ,
S(бок прав. призмы)=3*2√3*3√3 = 54 ( ед²) ,