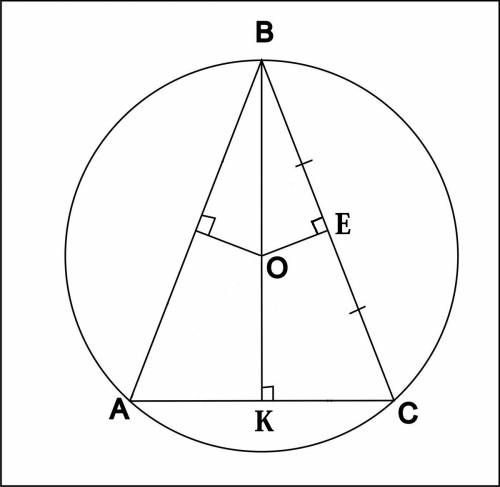
Радиус основания цилиндра равен 13 см, площадь сечения цилиндра плоскостью, параллельной оси цилиндра, равна 80 см², расстояние от плоскости сечения до оси цилиндра равно 12 см. Найдите высоту цилиндра
.
ответ: 8 см
Объяснение:
OA = OD = R = 13 см
Проведем ОН⊥AD. ОН лежит в плоскости основания, АВ - перпендикуляр к плоскости основания, значит ОН⊥АВ.
Тогда ОН⊥(АВС),
ОН = 12 см - расстояние от оси цилиндра до плоскости сечения.
ΔАОН: ∠АНО = 90°, по теореме Пифагора
АН = √(АО² - ОН²) = √(13² - 12²) = √(169 - 144) = √25 = 5 см
ОН - высота равнобедренного треугольника AOD, значит ОН и медиана, ⇒
AD = 2АН = 10 см
ABCD - прямоугольник,
Sabcd = AD · АB = 80
АB = Sabcd : AD = 80 : 10 = 8 см
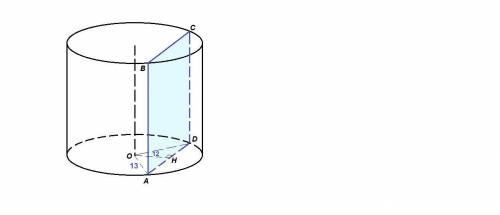
проведём прямую через точку Д параллельную стороне АВ, которая пересекает сторону ВС в точке К. т.к. прямые АВ и ВЛ параллельны и ЕД, ВК секущие,
т.к. прямые ЕД и ВС параллельны и ЕВ, Дк секущие, то
ДЕВ+КДЕ=180
ЕВК+ВКД=180
ДЕВ+ЕВК=180
КДЕ+ВКД=180 =>
КДЕ=ЕВК , ВКД=ДЕВ
т.к ЕВК=КДЕ, то ВД - биссектриса ЕВК и КДЕ => ЕВД=ДВК=ВДЕ=ВДК
т.к. ЕВД=ВДК, то треугольник ЕВД - равнобедренный => ДЕ=ВЕ
ч.т.д.