Объяснение:
Очевидно, что внутри отрезка AB такой точки существовать не может (если бы существовало, тогда сумма двух меньших отрезков должна быть больше длины исходной, что является противоречием), поэтому эта точка должна лежать где-то за пределами отрезка (по условию же сказано, что нужно найти точки на прямой, а не внутри отрезка).
Пусть l - расстояние от искомой точки X до A, тогда l + 6 - это расстояние от X до B. Тогда справедливо уравнение:
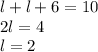
Значит, точка X должна отстоять от точки A на 2 см
Выглядит схематично это так:
2см 6см
---------------|----------------|------------------------------------------|----------------->
X A B
Это справедливо и для случая:
6см 2см
------------------|------------------------------------------|-------------|--------->
A B X
Больше таких точек нет.
Пусть неизвестный катет равен -х неизвестная гипотенуза y
Тогда можно записать, что х+у=25
По теореме Пифагора для прямоугольного треугольника
y^2=x^2+15^2
Получили систему уравнений
{x+y=25
{y^2 =x^2+225
Из первого уравнения вырази х и подставим во второе уравнение x=25-y
y^2=(25-y)+225
y^2=625-50y+y^2+225
50y =850
y=850/50=17
Гипотенуза равна 17 дм
найдем второй катет
х=25-у=25-17 =8 дм
Второй катет равен 8 дм
Найдите гипотенузу с,катет b и угол "бета" прямоугольного треугольника по катету а=7 дм и противолежащему углу "альфа"=56 (градусов)
В прямоугольном треугольнике найдем угол "бетта"
"бетта" =180-90-"альфа" =90-56=34(градуса)
Определим длину гипотенузы с по длине катета а и прилежащему углу
с = а/cos(альфа) =7/cos(34) = 8,44 дм
Определим длину катета по длине катета а и углу "альфа"
b=a*tg(альфа) =7*tg(34) =4,72 дм