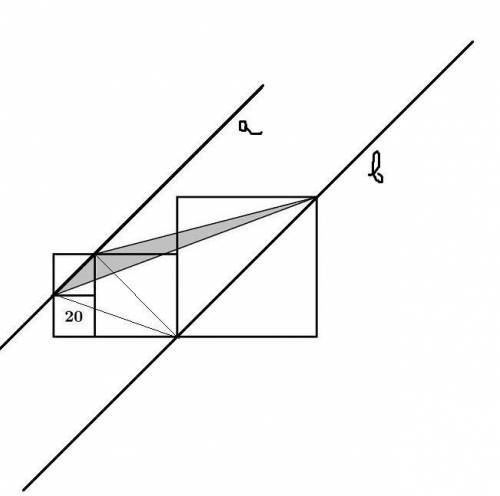
Рассмотрим множество треугольников, у которых две вершины расположены на диагонали маленького квадрата (на исходном рисунке в условии), а третья лежит на прямой, содержащей диагональ большого квадрата (см. мой рисунок). Заметим, что площади треугольников, входящих в это множество, попарно равны. Действительно, у всех треугольников общая сторона — диагональ малого квадрата, высоты, падающие на эту диагональ тоже равны, поскольку a ║ b.
Значит, площадь серого треугольника равна площади треугольника, указанного на моем рисунке. Площадь среднего квадрата равна 80. Теперь осталось следить за руками: (80+20+20)-40-10-60/2=70-30=40. Площадь равна 40.
1) Периметр - линейная величина, значит отношение периметров подобных тр-ков равно отношению соответствующих сторон этих тр-ков: 7:5.
2) пусть меньшая сторона одного тр-ка равна х, а меньшая сторона второго тр-ка - х1. Тогда х:х1=7:5, тогда х1=(5х)/7. По условию: х+х1=36, значит х+((5х)/7)=36, (12х)/7=36, х=21 (см), а х1=(5*21)/7=15 (см).
3) В одном тр-ке стороны относятся как 3:7:8 и меньшая из них равна 21 см. Тогда 3k=21, k=7, где k- коэффициент пропорц-сти для этого тр-ка. Две другие стороны соответственно равны: 7*7=49 и 8*7=56 см. Это "больший" треугольник.
4) В "меньшем" тр-ке меньшая сторона равна 15 см (см. пункт 1), что равно 3t, где t- коэф-нт пропорциональности этого тр-ка. Получим, что t=5, тогда вторая сторона равна 7*5=35 см, а третья 8*5=40 см.
ОТВЕТ: 21, 49, 56 см и 15, 35, 40 см.
ответ: смотри рисунок
Объяснение: