Задача с таким условием наверняка дается с рисунком, который должен быть приложен.
ответ: а) 24,2 м²; б) 34,848 м²; в) 8,712 м²
Объяснение:
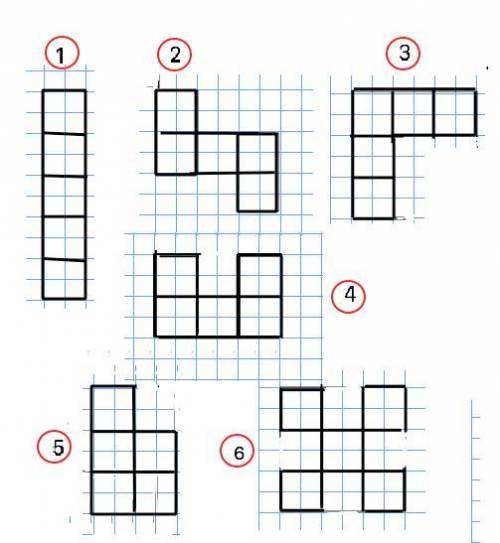
Количество n свободных сторон, участвующих при измерении периметра, при различном расположении пяти квадратных участков двора может быть разным. (см. рисунок приложения)
Тогда длина стороны квадрата а=P:n, Ѕ (двора)=5•а²
а) № 1, 2, 3, 4 – n=12 ⇒ a=2640:12=220 cм=2,2 м ⇒ Ѕ=5•2,2² =24,2 м²
б) №5 – n=10. ⇒ а=2,64м ⇒ Ѕ= 5•2,64² =34,848 м²
в) №6 – n=20 ⇒ а=1,32 м ⇒ Ѕ=5•1,32² =8,712 м²
ответ: a) 62°; б) 118°
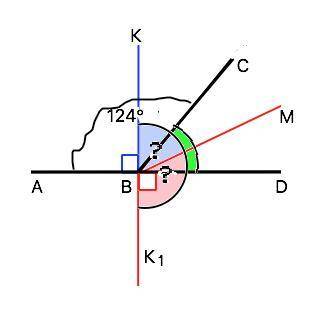
Объяснение: Вопрос явно неполный - не указан второй угол. Правильно: Углы ABC и BCD – смежные, причем угол ABC равен 124 градуса. Найдите угол между перпендикуляром, проведенным из точки B к прямой AD и биссектрисой угла CBD.
* * *
Сумма смежных углов 180°, поэтому ∠СВD=180°- ∠ABC=180°-124°=56°.
Обозначим биссектрису угла СВD как ВМ. Биссектриса угла делит его пополам, поэтому ∠СВМ=∠DBM=56°:2=28°
У задачи 2 варианта решения.
а) Перпендикуляр ВК к прямой AD лежит в той же полуплоскости, что луч ВС. Тогда искомый угол КВМ=∠КВD-∠MBD=90°-28°=62°
б) Перпендикуляр ВК1 лежит во второй полуплоскости. Тогда искомый угол К1ВМ=∠K1BD+∠DBM=90°+28°=118°
Для треугольника МКР окружность 2 (центр О2, радиус r) - вписанная, а окружность 1 (центр О1, радиус ρ) - вневписанная (то есть касается стороны КР и продолжений сторон МК и МР). Площадь треугольника МКР обозначена S, площадь A1B1C1 - S1; площадь А2В2С2 - S2; R - радиус описанной вокруг МКР окружности. Углы треугольника МКР обозначены так α = угол КРM; β = угол PКМ;γ = угол КМР;
Очевидно, что ( :) ) угол А2О2В2 = угол А1О1В1 = 180° - γ; угол С1О1В1 = α; (оба угла составляют 180° в сумме с углом B1PC1... или, если хочется, стороны этих углов перпендикулярны попарно...) угол С2O2B2 = 180° - α; аналогично угол A1O1C1 = β; угол A2O2C2 = 180° - β;
Далее, площадь треугольника A2B2C2 равна сумме площадей треугольников O2A2B2; O2B2C2 и O2C2A2; отсюда S2 = (r^2/2)*sin(α) + (r^2/2)*sin(β) + (r^2/2)*sin(γ) = r^2*(sin(α) + sin(β) + sin(γ))/2;
Площадь треугольника A1B1C1 равна сумме площадей треугольников O1B1C1 и O1C1A1 минус площадь треугольника O1A1B1; отсюда S1 = (ρ^2/2)*sin(α) + (ρ^2/2)*sin(β) - (ρ^2/2)*sin(γ) = ρ^2*(sin(α) + sin(β) - sin(γ))/2;
(Примечание: не стоит забывать, что sin(Ф) = sin(180° - Ф) :) )
По теореме синусов, КР = 2*R*sin(γ); MP = 2*R*sin(β); MK = 2*R*sin(α);
Если обозначить p - полупериметр MKP, то
sin(α) + sin(β) + sin(γ) = p/R; sin(α) + sin(β) - sin(γ) = (p - KP)/R;
Поскольку S = p*r = (p - KP)*ρ; (а вот должны знать :)) то
sin(α) + sin(β) + sin(γ) = S/(r*R); sin(α) + sin(β) - sin(γ) = S/(ρ*R);
и получается окончательно
S1 = (ρ^2/2)*S/(ρ*R) = S*ρ/(2*R); S2 = S*r/(2*R); и S2/S1 = r/ρ; чтд.