y = 2sinx + 1
Объяснение:
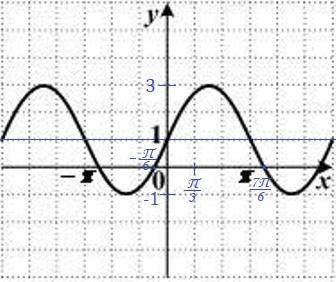
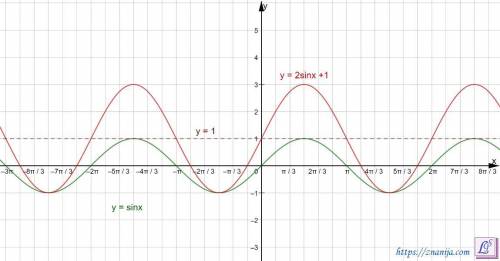
На рисунке изображен график функции y = 2sinx + 1
График функции y = sinx сдвинут относительно оси Y на +1 единицу, коэффициент растяжения вдоль оси Y = 2.
Свойства функции y = 2sinx + 1.
Функция y = 2sinx + 1 периодическая, период T = 2π
Ось Y пересечена в т.(0; 1 ):
x = 0; y = 2*sin0 + 1 = 2 * 0 + 1 = 1
Нули функции:
y = 0; 2sinx+1 = 0; sinx = -1/2
x₁ = arcsin(-1/2) + 2πn = 7π/6 + 2πn; n∈Z
x₂ = π - arcsin(-1/2) + 2πn = π - 7π/6 + 2πn = -π/6 + 2πn; n∈Z
Максимальное значение функции y = 2 * 1 + 1 = 3 (т.к. максимальное значение функции sinx = 1)
Минимальное значение функции y = 2 *(-1) + 1 = -2 + 1 = -1 (т.к. минимальное значение функции sinx = -1).
1.Пусть одна сторона равна х, тогда другая 6х. У параллелограмма противолежащие стороны равны. Сумма сторон равна 84. Тогда составим уравнение
х+х+6х+6х=84
14х=84
х=84:14
х=6
Тогда 6х=6×6=36
Проверка: 6+6+36+36=84
ответ: 6; 6; 36; 36
2.В прямоугольнике противоположные стороны равны. Значит ВС=АD=18см
BD и АС являются диагоналями прямоугольника ABCD.
Диагонали в прямоугольнике равны, т.е BD=АС=22см
О-точка пересечения диагоналей, которая делит их пополам. Значит ОD=ОА=ОВ=ОС=1/2 BD=11см
Рboc=ОB+ОC+ВC
Рboc=11+11+18=40см
3.диагонали ромба являются биссектрисами его углов (то есть делят их пополам);
сумма соседних углов ромба равна 180°;
противоположные углы ромба равны
4.Диагональ АС делит параллелограмм на 2 подобных треугольника. Углы NAB=PCD, угол ABN=CDP и следовательно углы BNA= СPD, отсюда следует что прямоугольники ABN и CDP также подобны. Следовательно прямые BN и PD равны между собой. Что и требовалось доказать
5.Примем коэффициент отношения AF:FD=a. Тогда AF=a, FD=5a. Их сумма 6а=18 см, ⇒ а=18:6=3 см. Отрезок АF=3 см, отрезок FD=5•3=15 см АВСD - параллелограмм. ВС║AD, CF – секущая. ∠ВСF=∠СFD как накрестлежащие. Но ∠FCD=∠BCF (СF – биссектриса) ⇒ ∠CFD=∠FCD . Углы при основании FC треугольника FDC равны, следовательно, он равнобедренный и CD=FD=15 см ( свойство). Запомним: Биссектриса угла параллелограмма отсекает от него равнобедренный треугольник. Противоположные стороны параллелограмма равны, ⇒ АВ=CD=15 см. Периметр =сумма всех сторон АВСD. Р=2•(18+15)=66 см