
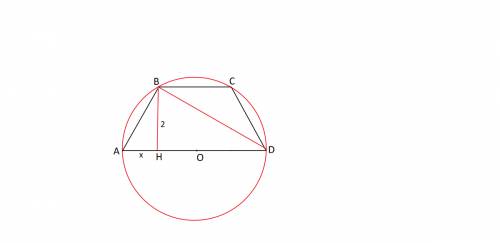
Сделаем рисунок согласно условию задачи.
Проведем в трапеции высоту ВН и диагональ ВD.
Так как АD - диаметр окружности, в которую трапеция вписана,
треугольник АВD- прямоугольный ( угол АВD опирается на дугу 180 градусов).
Площадь трапеции равна произведению ее высоты на полусумму оснований.
S ABCD=BH(BC+AD):2
2S=BH(BC+AD)
(BC+AD)=2S:BH
(BC+AD)=16:2=8
--------------------------------------------------------
Высота равнобедренной трапеции, проведенная из вершины тупого угла, делит большее основание на два отрезка, меньший из которых равен полуразности оснований, а больший – полусумме оснований.
--------------------------------------------------------
Обозначим отрезок АН =х, а
НD= полусумме оснований и равен 4
-------------------------------------------------------
Высота прямоугольного треугольника, проведенная из вершины прямого угла, есть среднее пропорциональное между отрезками, на которые делится гипотенуза этой высотой..
------------------------------------------------------
Cледовательно,
ВН²=АН*НD
4=4х
х=1
AD=1+4=5
R=AO=5:2=2,5
аргумент функции --- это переменная (х)
график линейной функции --- прямая линия
для построения прямой достаточно двух точек
(точка на плоскости имеет две координаты х и у))):
если х любое выбрать,
то у можно вычислить по формуле (выражение для функции)))
у Вас написано у = -1/3 ((возможно Вы пропустили х)))
если у = -(1/3)*х
берем х = 3, вычисляем у = -1
берем х = -6, вычисляем у = 2
и строим прямую, проходящую через эти две точки...
а если функция задана как написано: у = -1/3
то это прямая линия, параллельная оси ОХ и
проходящая через точку (1/3) на оси ОУ