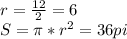
Какие из указанных векторов перпендикулярны?
1) a {2; -6} и b {1; -3} ; 2) m {3; 9} и n {6; -2} ;
3) c {-2; 3} и d {6; 9} ; 4) h {5; -6} и l {5; 6}.
Объяснение:
Два вектора перпендикулярны если их скалярное произведение равняется нулю , х₁*х₂+у₁*у₂=0
1) a {2; -6} и b {1; -3} ,2*1+(-6)*(-3)=20 , 20≠0 , не перпендикулярны ;
2) m {3; 9} и n {6; -2} ;3*6+9*(-2)=18-18=0 , m⊥n ;
3) c {-2; 3} и d {6; 9} , -2*6+3*9=-12+27=15 , 15≠0 , не перпендикулярны ;
4) h {5; -6} и l {5; 6} , 5*5+(-6)*6=25-36=-11 ,-11≠0 ,не перпендикулярны ;
3) Если четырёхугольник вписан в окружность, то суммы величин его противоположных углов равны 180°.
Так как углы, взятые в порядке следования относятся как 1:3:4 , то ∠А=х , ∠В=3х , ∠С=4х и ∠А+∠С=х+4х=5х=180° , х=36° .
∠А=36° , ∠В=3*36°=108° , ∠С=4*36°=144°
Сумма внутренних углов четырёхугольника равна 360°.
∠D=360°-36°-108°-144°=72°
Или ∠В+∠D=5х , ∠D=5x-∠B=3x-3x=2x , 2x=2*36°=72° .
4) Сторона правильного треугольника равна  .
.
Радиус вписанной окружности в прав. тр-к равна 1/3 его высоты, то есть 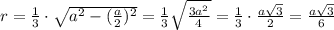 .
.
Сторона прав.четырёхугольника - квадрата, описанного около окружности, равна 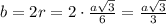 .
.
Периметр квадрата равен 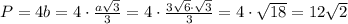 см.
см.