Заметим, что треугольники ABD и CBD - равносторонние и равны. Легко доказать, что высоты BH и BF пересекаются под углом 60 градусов. При этом эти высоты равны, как высоты в равных друг другу равносторонних треугольниках. Значит, треугольник HBF - равносторонний. Сторона его равна 12/3=4 см. Тогда легко найти и сторону ромба, как гипотенузу треугольника ABH с известным катетом BH и углом A=60. AB= HB/(корень из 3 пополам) . Тогда площадь ромба будет равна произведению высоты на сторону: 3*3/(корень из 3 пополам) =6*(корень из трёх) . Здесь * - знак умножения.
1)Найдём BP и AK по теореме Пифагора:
BP=√BO²-OP²=√33²-22²=11√5
AK=√AO²-OK²=√77²-22²=33√5
Отсюда можно найти AB=33√5+11√5=44√5
2)Заметим, что BH=BP(как отрезки касательных,проведённых из одной точки)
Вспомним, что центр вписанной окр.-точка пересечения биссектрис треугольника, поэтому найдём синус угла ABC, используя этот факт:
sin2α=2sinαcosα=2*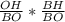 =
=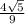
Пусть CP=CK=x,
Тогда SΔ=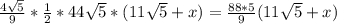
С другой стороны, SΔ=S(ABO)+S(AOC)+S(BOC)
SΔ=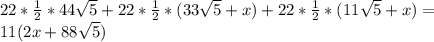
Приравнивая два вышенаписанных выражения для площади, найдём, что x=16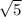 .
.
3)Тогда CO можно найти по теореме Пифагора:
CO=√OK²+CK²= √196*9=42