У меня с украинским не очень, поэтому...
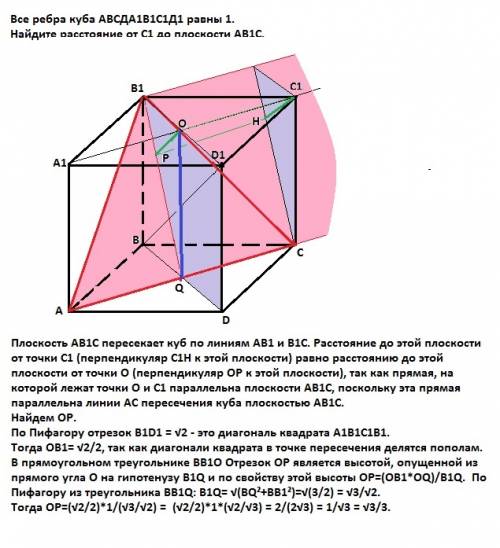
Одна из основ трапеции на 12 см больше другой а периметр трапеции равен 52 см (см. рис). Диагональ трапеции делит острый угол пополам. Установите соответствие между отрезком и его длиной
Отрезок:
1. Меньшее основание трапеции
2. Большая основа трапеции
3. Высота трапеции
4. Средняя линия трапеции
Длина:
А) 8 см
Б) 10 см
В) 16 см
Г) 20 см
Д) 22 см
------------
Биссектриса острого угла трапеции отсекает от трапеции равнобедренный треугольник. Если эта биссектриса является и диагональю трапеции, то малое основание трапеции боковой стороне
В условии задания не сказано, что трапеция равнобедренная, но все цифирки даны именно из этого предположения!
Считаем трапецию равнобедренной. Тогда из условия, что одно основание длиннее другого на 12 см получаем
x + x + x + x + 12 = 52
x = 10 см
1. Меньшее основание трапеции
ВС = x = 10 см
2. Большее основание трапеции
АД = х + 12 = 10 + 12 = 22 см
3. Высота находится сложнее
Проекции боковых рёбер на основание равны
АГ = ЕД
ГЕ = 10 см
АД = АГ + ГЕ + ЕД = 2*АГ + 10 = 22
2*АГ = 12
АГ = 6 см
По т. Пифагора
АВ² = АГ² + ВГ²
10² = 6² + ВГ²
100 = 36 + ВГ²
ВГ² = 64
ВГ = 8 см, и это высота
4. Средняя линия трапеции равна половине суммы оснований
(ВС + АД)/2 = (10 + 22)/2 = 16 см
----------------------
Но в условии ошибка, для трапеции с неравными боковыми сторонами всё не так.
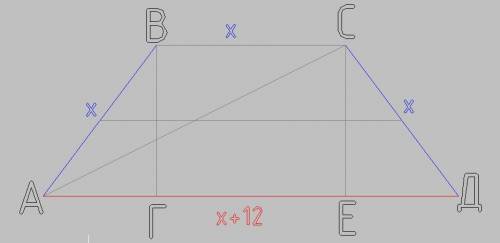
Площадь трапеции в основании равна произведению высоты на среднюю линию.
Высота трапеции равна высоте треугольника АВК, где ВК =с. а АК=d-b=17cm.
h=(2V(p(p-a)(p-c)(p-(d-b)))/(d-b)=(2V(34(34-26)(34-25)(34-17))/17=24 см.
Lср=39+22/2=30,5 см. So=24*30,5=732 cm^2
Высоту призмы можно найти, разделив площадь сечения АА1С1С на диагональ АС. Если провести вторую высоту СМ, получим два прямоугольных треугольника – АСМ и СМД. ДМ = V(c^2-h^2)=V(25^2-24^2)=7 cm. AM=39-7=32 cm. AC=V(32^2+24^2)=V(1024+576)=40 cm. Высота призмы равна 400/40=10 см. Объём прихмы равен 732*10=7320 см^3.