Варіант 1 1. Перетворення f трикутника ABC є таким, що f(А) = В, 1 (B) = C, f (C) = А, а для будь-якої - id1736928420210803 от сонька2005бедовая 03.08.2021 07:32

Question

Геометрия: Варіант 1 1. Перетворення f трикутника ABC є таким, що f(А) = В, 1 (B) = C, f (C) = А, а для будь-якої точки Х трикутника ABC, відмінної від точок А, В і С, виконується рівність f(x) = Х. Чи є перетворення f тотожним? 2. Опишіть яке-небудь перетворення фігури, яка складається з усіх точок сторін трикутника, при якому і образом е коло, вписане в даний трикутник. 3. Кожній точці графіка функції у=х2 ставиться у відпо- відність її проекція на: 1) вісь абсцис; 2) вісь ординат. Чи є дане перетворення

сонька2005бедовая · Accepted Answer

Для начала найдем отношение ВР/РС. Для этого:
Проведем BD параллельно АС. Тогда <PAC=<BDA, как накрест лежащие при параллельных прямых BD и AC и секущей АD.
∆АКМ ~ ∆BKD по двум углам (1).
∆АРС ~ ∆DРВ по двум углам (2).
Из (1) BD/AM=4 и BD=4AM = 2AC.
Из (2) BP/PC=2.
ВМ - медиана и по ее свойствам Sabm=Scbm.
Треугольники АВК и АКМ - треугольники с общей высотой к стороне ВМ. Значит Sabk/Sakm=4/1. => Sabk=Sabc*(1/2)*(4/5)=(2/5)*Sabc.
Sakm=Sabc*1/(2*5)=(1/10)*Sabc.
Треугольники ABP и APC - треугольники с общей высотой к стороне ВC.
Значит Sabp/Sapc=2/1. => Sapc=Sabc*1/3=(1/3)*Sabc.
Тогда Skpcm=Sapc-Sakm = (1/3)*Sabc-(1/10)*Sabc = (7/30)*Sabc.
Sabk/Skpcm=(2/5)/(7/30)=12/7.

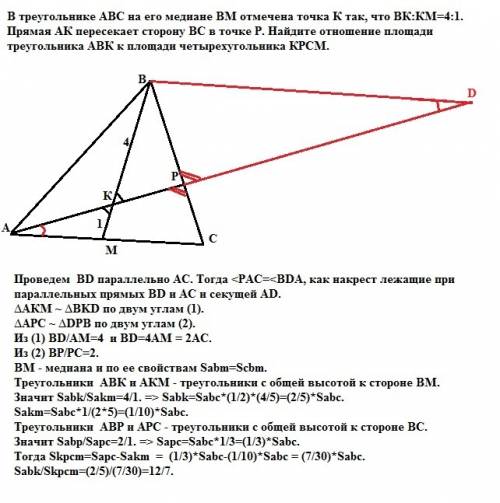
Втреугольнике авс на его медиане вм отмечена точка к так, что вк: км=4: 1. прямая ак пересекает стор

Втреугольнике авс на его медиане вм отмечена точка к так, что вк: км=4: 1. прямая ак пересекает стор

MOGZ ответил