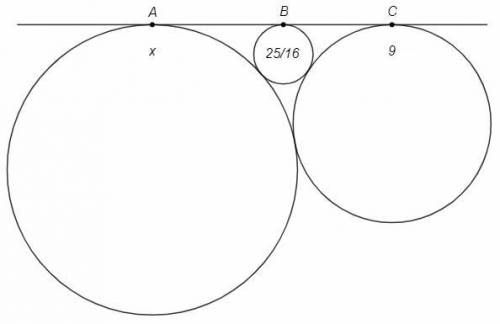
Две окружности касаются внешним образом и имеют общую внешнюю касательную. Найдем расстояние между точками касания на прямой.
Отрезки касательных из одной точки равны (синие отрезки). Центры окружностей лежат на биссектрисах углов, образованных касательными. Угол между биссектрисами смежных углов - прямой. Точка касания окружностей лежит на линии центров. Радиусы, проведенные в точку касания, перпендикулярны касательной. Таким образом синий отрезок является высотой из прямого угла и равен среднему пропорциональному проекций катетов, √(R1*R2).
Расстояние между точками касания на прямой равно 2√(R1*R2).
В задаче три пары аналогичных окружностей.
AB+BC=AC => 2√(x*25/16) +2√(9*25/16) =2√(9x) <=> 7√x =15 <=> x=225/49

ну смотри, угол между прямой и плоскостью, это угол между её проекцией и этой прямой, у тебя же дан косинус угла, если его сократить получится 24/25, у тебя дан прилежащий катет, ты можешь найти гипотенузу:
24/25 = 48/x где - х это гипотенуза
x = 50
так как у тебя даже сказано "перпендикуляр" значит треугольник прямоугольный, ну по теореме пифагора найди, то есть гипотенуза в квадрате минус катет (который равен 48 по условию) в квадрате и всё это под корнем будет равно 14 ( ну это 50 в квадрате - 48 в квадрате и всё это под корнем)
вторая аналогично.
извиняюсь за текст, пишу с компа, телефон без зарядки)
ответ:
объяснениe ae и сe проведены к одной стороне ac то значит ce=ae=6(еще можно по равенству треугольников(сторона и два приежащие к ней угла).проводим дополнительную диагональ,она делит ее пополам полукчаются две части по 4,5.по теореме пифагора находим часть диагонали и саму диагональ затем находим те частиае и дф и по теореме ипифагора находим одну сторону потом другую