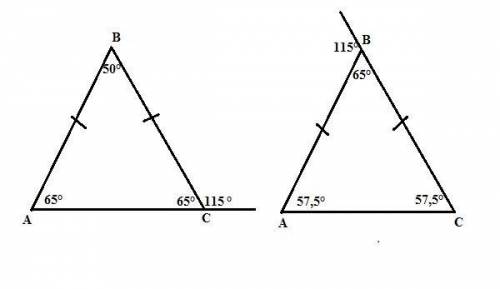
1. 65°, 65°, 50°.
2. 57,5°; 57,5°; 65°.
Объяснение:
Нам дан один из внешних углов равнобедренного треугольника. У равнобедренного треугольника углы при основании равны.
Значит возможны два варианта решения:
1. Если дан внешний угол при основании, то внутренний, смежный с ним, равен 180° - 115° = 65° (сумма смежных углов равна 180°).
Тогда угол при вершине треугольника равен 180° - 2·65° = 50° (по сумме внутренних углов треугольника, равной 180°).
ответ: 65°, 65°, 50°.
2. Если дан внешний угол при вершине, то внутренний, смежный с ним, равен 180° - 115° = 65° (сумма смежных углов равна 180°).
Внешний угол треугольника равен сумме двух внутренних (в нашем случае равных), не смежных с ним углов. Следовательно, углы при основании такого треугольника равны 115°:2 = 57,5°.
ответ: 57,5°; 57,5°; 65°.
1)отмечаешь точку Е, как середину А1В1
2)проводишь линию из А в точку Е
3)проводишь линию из точки Е к стороне В1С1 так, чтобы эта линия была параллельна АС. Ставишь точку F на В1С1 в месте пересечения Т.е. F ставишь в середине В1С1.(Сечение образуется путём пересечения плоскости с призмой. Т.к. эта плоскость пересекает два параллельных друг другу основания, то отрезки пересечения должны быть параллельны друг другу. Т.к. АС параллельно А1С1, то в EF должно быть параллельно А1С1. Точка F должна делить В1С1 на отрезки в том же соотношении, что и точка Е сторону А1В1, т.е пополам).
4)Соединяешь F с точкой С.
Всё, у тебя готово сечение
из формулы площади S=(a+b)*h/2
b=2*45/5-7= 11см