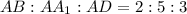 .
.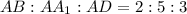 можно положить:
можно положить: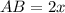 ;
;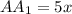 ;
;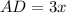 ;
;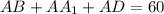 ;
; ;
;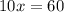 ;
; ;
;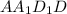 и расчитываем на ней диагональ по Теореме Пифагора;
и расчитываем на ней диагональ по Теореме Пифагора;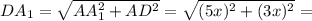
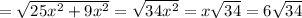 ;
;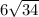 ;
;
МВ - перпендикуляр к плоскости прямоугольника, тогда
ВА - проекция наклонной МА на плоскость (АВС), значит
∠МАВ = 45°,
ВС - проекция наклонной МС на плоскость (АВС), значит
∠МСВ = 30°.
а) ВА⊥AD как стороны прямоугольника, ВА - проекция МА на (АВС), значит МА⊥AD по теореме о трех перпендикулярах, значит
ΔMAD прямоугольный.
ВС⊥CD как стороны прямоугольника, ВС - проекция МС на (АВС), значит МС⊥CD по теореме о трех перпендикулярах, значит
ΔMCD - прямоугольный.
б) ΔМВА прямоугольный с углом 45°, значит равнобедренный,
АВ = МВ = 4 см
ΔМВС: ∠МВС = 90°,
tg ∠MCB = MB / BC
tg30° = 4 / BC
BC = 4 / (1/√3) = 4√3 см
в) ΔBDC - прямоугольный,
Sbdc = BC · CD / 2 = 4 · 4√3 / 2 = 8√3 см²
(тангенс угла - это отношение противолежащего катета к прилегающему)
находим tg(<A)=BC/AB=3/1
tg(<C)=AB/BC=1/3
имеем два прямоугольных треугольника АНВ и ВНС
tg(<C)=ВН/НС=1/3
tg(<A)=ВН/АН=3/1
теперь находим отношение АН/НС = [tg(<C)] / [tg(<A)] = (ВН/НС) / (ВН/AH) = (1/3) / (3/1) = 1/3*1/3 = 1/9
(рисунок во вложении)