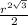C другой стороны площадь этого треугольника можно найти как половина произведения основания на высоту, т.е. 2r *h. приравняем эти площади и находим h.
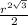C другой стороны площадь этого треугольника можно найти как половина произведения основания на высоту, т.е. 2r *h. приравняем эти площади и находим h.
62π см²
Объяснение:
Диагонали прямоугольного параллелепипеда равны, пересекаются в одной точке и делятся ею пополам.
Значит все вершины параллелепипеда находятся на одинаковом расстоянии от точки пересечения диагоналей, т.е.
точка пересечения диагоналей - центр описанной сферы, а половина диагонали - ее радиус.
Квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов трех его измерений:
d² = 2² + 3² + 7² = 4 + 9 + 49 = 62
d = √62 см
r = d/2 = √62/2 см
S = 4πr² = 4 · π · (√62/2)² = 4 · π · 62/4 = 62π см²