Разъясним условие. Нам дана прямая l, некоторое расстояние к. Если взять точку А так, чтобы расстояние между взятой точкой а прямой l было равно к, то прямая, проходящая через точку А и параллельная прямой l является геометрическим местом всех точек, удовлетворяющих условию. (Обозначим эту прямую буквой m).
Возьмем точку В, не лежащую на прямой m. Пусть перпендикуляр к прямой l пересекает прямую m в точке С, а прямую l в точке D. CD = k, т.е. чтобы точка В удовлетворяла условию, она должна лежать на прямой m.
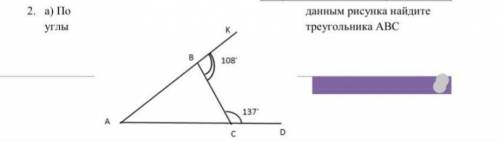
AK - Прямая линия, или угол 180°.
Угол В + 108° = 180°.
Угол В = 180° - 108°
Угол В = 82°
AD также прямая линия.
Угол С + 137° = 180°
Угол С = 180°-137°
Угол С = 43°
Сумма всех углов треугольника 180°.
Угол А + 43° + 82° = 180°
Угол А + 125° = 180°
Угол А = 180°-125°
Угол А = 55°