Объяснение:
попытка N2
геометрическая интерпретация задачи
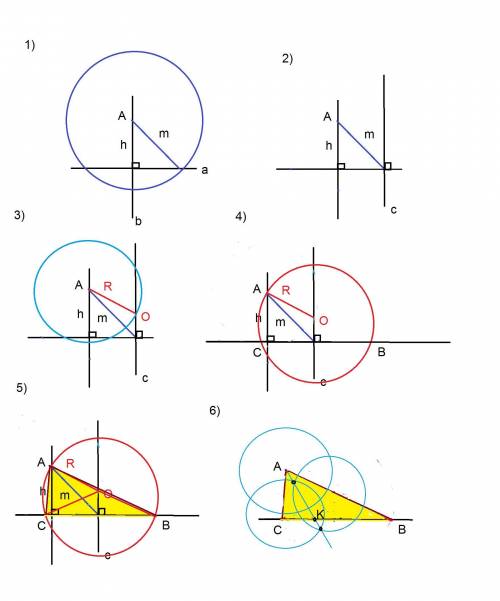
построить биссектрису треугольника по высоте h, медиане m, радиусу описанной окружности
(без описания элементарных построений)
1) строим 2 перпендикулярные прямые. на вертикальной откладываем высоту. Верхняя точка высоты - Вершина А треугольника.
из вершины как центра строим окружность радиуса = m
2) через точку пересечения медианы и горизонтальной прямой строим перпендикуляр к горизонтали (это прообраз серединного перпендикуляра к основанию треугольника)
3) из вершины А строим окружность радиуса R
точка пересечения этой окружности с перпендикуляром с будет центром описанной окружности О
4) строим окружность с центром О радиуса R
точки пересечения этой окружности с горизонтальной прямой - Вершины треугольника С и B
5) соединяем точки А, В, С
6) строим биссектрису АК угла А треугольника
готово.
P/S.
Теперь дело за формулами.
Возможно геометрическая интерпретация найти алгебраическую.
Если геометрическая интерпретация не совсем то что надо отметьте как нарушение.
В любом случае автору за интересную задачу
продолжение следует....
С линейки проводим прямую и на ней с циркуля отложим отрезок АВ, равный отрезку МК. Для этого произвольно на прямой ставим точку А, с циркуля измеряем отрезок МК и строим окружность с центром в точке А радиуса МК (всю окружность строить необязательно, смотри, выделенное красным цветом). Точку пересечения окружности с прямой обозначаем В.
Далее строим угол ВАF равный углу 1. Для этого строим с циркуля окружность радиуса МК с центром в вершине угла 1 (всю окружность строить необязательно, смотри, выделенное красным цветом). Точки пересечения данной окружности со сторонами угла 1 обозначаем N и Р.
С циркуля измеряем длину отрезка NP и строим окружность радиуса NP с центром в точке В (всю окружность строить необязательно, смотри, выделенное синим цветом). Точку пересечения окружности с окружностью радиуса МК с центром в точке А обозначаем F.
Далее, проводим луч АF с линейки.
Далее, строим угол АВD равный углу 2. Для этого строим с циркуля окружность радиуса МК с центром в вершине угла 2 (всю окружность строить необязательно, смотри, выделенное красным цветом). Точки пересечения данной окружности со сторонами угла 2 обозначаем О и Е.
С циркуля строим окружность радиуса МК с центром в точке В (всю окружность строить необязательно, смотри, выделенное красным цветом), затем измеряем длину отрезка ОЕ и строим окружность радиуса ОЕ с центром в точке А (всю окружность строить необязательно, смотри, выделенное синим цветом). Точку пересечения данных окружностей обозначаем D.
Далее, проводим луч ВD с линейки.
Точку пересечения лучей АF и ВD обозначаем С. Получаем треугольник АВС, в котором по построению АВ = МК, ВАС =1, АВС =2, следовательно, треугольник АВС - искомый.
Данная задача не всегда имеет решение. Так как по теореме о сумме углов треугольника: сумма углов всякого треугольника равна 1800. Значит, сумма двух данных углов должна быть меньше 1800. Если же сумма двух данных углов будет больше 1800, то нельзя построить треугольник, углы которого равнялись бы данным углам.
Объяснение: