Внутри круга дана точка м отстоящая от центра на 5 см. через эту точку проведена хорда ав так, что ам=6 см, а мв=9см. тогда радиус круга равен

👇

Ответ:

Ilonka2734

25.04.2022

Через точки М и О(О-центр окружности) проведем прямую, чтоб она пересекала окружность в двух местах, пункты пересечения обозначим К и Т
КТ - диаметр окружности(КТ проходит через пункт О, - центр окружности)
ОМ = 5 (по условию)
Обозначим КМ через х,
ОТ = ОК = МО +МК = 5+х

При пересечении двух хорд окружности, получаются отрезки, произведение которых у одной хорды равно произведению отрезков другой хорды
значит КМ* МТ = АМ * АВ
х*(х+5+5) = 6*9
х^2+10x=54
имеем квадратное уравнение:
x^2 +10x- 54=0
D = 10^2 + 216 = 316; √D=2√79
x1 = -b + √D /2a = -10 +2√79/2 = -5+√79
x2 = -b -√D/2a = (тут можно не считать получится отрицательное число, а длинна не может быть отрицательной)
КМ =х= -5 +√79
КО = 5 + (-5) +√79=√79 (это и есть радиус)
Внутри круга дана точка м отстоящая от центра на 5 см. через эту точку проведена хорда ав так, что а

Внутри круга дана точка м отстоящая от центра на 5 см. через эту точку проведена хорда ав так, что а

4,4(87 оценок)

Открыть все ответы

Ответ:

taroslav

25.04.2022

Пусть катеты треугольника равны a и b, 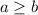$a\ge b$ . Воспользовавшись теоремой Пифагора и выражением площади через катеты, получаем систему

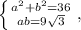
$\left \{ {{a^2+b^2=36} \atop {ab=9\sqrt{3}}} \right. ,$

решив которую, находим a и b: 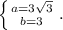$\left \{ {{a=3\sqrt{3}} \atop {b=3}} \right. .$

При решении можно было бы выразить одну букву через другую, а можно и так: удваиваем второе уравнение, после чего добавляем его к первому, а также вычитаем его из первого, замечая при этом, что возникают формулы "квадрат суммы" и "квадрат разности":

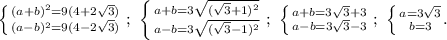
$\left \{ {{(a+b)^2=9(4+2\sqrt{3})} \atop {(a-b)^2=9(4-2\sqrt{3})}} \right. ;\ \left \{ {{a+b=3\sqrt{(\sqrt{3}+1)^2}} \atop {a-b=3\sqrt{(\sqrt{3}-1)^2}}} \right. ;\ \left \{ {{a+b=3\sqrt{3}+3}} \atop {a-b=3\sqrt{3}-3}} \right.;\ \left \{ {{a=3\sqrt{3}} \atop {b=3}}. \right.$

Меньший катет b=3 лежит против меньшего угла, поэтому на картинке это катет AC. Поэтому треугольник ADC равносторонний, угол CAD равен 60 градусам (здесь C - это вершина треугольника, а не основание биссектрисы). А поскольку угол CAC (первая C - это вершина треугольника, а вторая C - основание биссектрисы) равен 45 градусам, угол между медианой и биссектрисой будет равен 60-45=15 градусам.

ответ: A

4,4(20 оценок)

Ответ:

рана7

25.04.2022

Чертёж смотрите во вложении.

Дано:

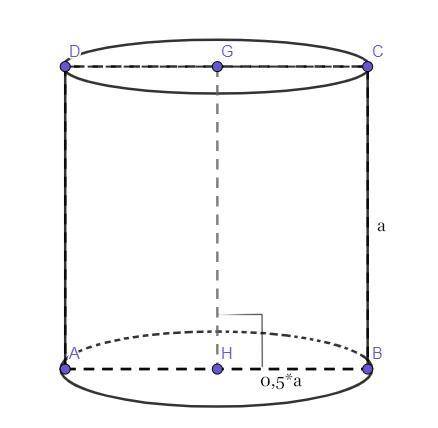
ABCD - квадрат и осевое сечение цилиндра.

СВ - сторона квадрата = а.

GH - высота цилиндра.

НВ - радиус основания цилиндра.

Объём цилиндра = объём шара.

Радиус шара = ?

Если осевое сечение цилиндра - квадрат, то радиус основания в два раза меньше этой стороны, а высота цилиндра равна стороне квадрата.

Следовательно -

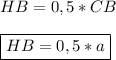
$HB=0,5*CB\\\\ \boxed{HB=0,5*a}$

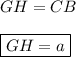
$GH=CB\\\\ \boxed{GH=a}$

Пусть V - объём цилиндра (и, также по условию задачи, шара), а r - радиус шара.

Объём цилиндра равен произведению площади основания цилиндра и её высоты.

То есть -

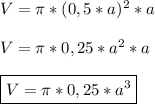
$V = \pi *(0,5*a)^{2} *a\\\\V = \pi *0,25*a^{2} *a\\\\ \boxed{V = \pi *0,25*a^{3}}$

Объём шара равен произведения куба радиуса, 4/3 и π.

То есть -

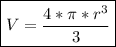
$\boxed{V = \frac{4*\pi *r^{3} }{3} }$

Написанные в рамках уравнения имеют одинаковые левые части. Поэтому, мы можем приравнять правые части уравнений и выразить переменную r -

$\boxed{ \boxed{\pi *0,25*a^{3}}= \boxed{\frac{4*\pi *r^{3} }{3} }}\\\\\\\ \pi *0,75*a^{3} =4*\pi *r^{3}\\\\0,75*a^{3} =4*r^{3} \\\\r = \sqrt[3]{0,1875*a^{3} }\\\\r=a\sqrt[3]{0,1875}$