108
Объяснение:
Так как у треугольника 2 стороны одинаковые значит это равнобедренный треугольник. Площадь такого треугольника вычисляется : 1/2 * а * h, где а - сторона основы, h - высота.
Проведем высоту из вершины в нашем треугольнике, и за т. Пифагора находим её:
h^2 = (15-9) * (15+9)
h^2 = 144
h = 12
S = 1/2 * a * h = 1/2 * 18 * 12 = 108
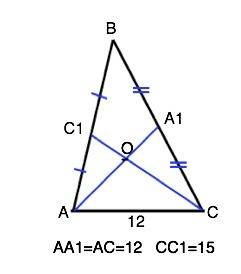
Медианы треугольника точкой пересечения делятся в отношении 2:1, считая от вершины. ⇒
АО=12:3•2=8
CO=15:3•2=10
Весь треугольник разделяется своими тремя медианами на шесть равновеликих (равных по площади) треугольников. Если провести медиану из В к АС, то
площадь ∆ АОС =2•1/6 S ABC=1/3 S ABC
По т.Герона площадь треугольника
S=√(р•(р-а)•(p-b)•(p-c), где а, b и c - стороны треугольника, р - его полупериметр.
р ∆ АВС=(12+8+10):2=15
По т.Герона S ∆AOC=√15•(15-8)•(15-10)•(15-12)
S ∆ AOC=√15•7•5•3=15√7⇒
S ∆ ABC=3•15√7=45√7 (ед. площади)
Вычислим по формуле Герона.
р = ½ × ( a + b + c).
P = ½ × 48 = 24 см.
S = √р × (р-а) × (p-b) × (p-c) = √24×9×9×6=√11664= 108см².
ответ: S треугольника = 108см².