
Дано: АВС- равнобедренный треугольник.
АМ- медиана.(18.4)
Р треугольника АВМ=79.2
Найти: Р треугольника АВС
АМ является и бессектрисой и медианой и высотой (свойства равнобедренного треугольника.)
Следовательно: Угол А делиться пополам (так как АМ является бессектрисой.) Следовательно эти половинки ровны.
АМ-общая сторона.
ВА=АС (по условию так как треугольник АВС равнобедренный.)
Следовательно треугольники АВМ=АМС (по 1 признаку.)
Следовательно Р треугольника АВС равен.
(79.2-18.4)• 2
Все готово
Объяснение:
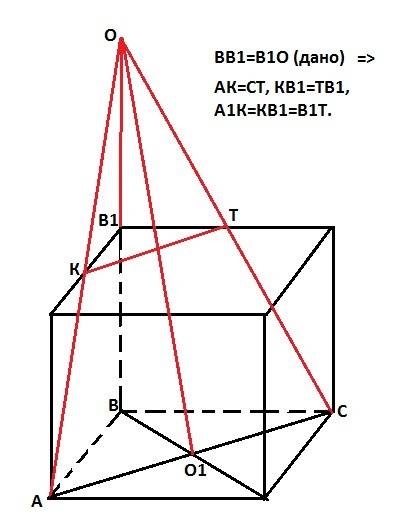
1. АВСD - квадрат. Диагонали квадрата взаимно перпендикулярны и точкой пересечения О1 делятся пополам. Следовательно, прямая ОО1 - перпендикулярна АС по теореме о трех перпендикулярах, так как ВО (перпендикулярная АС) - проекция наклонной ОО1. Тогда треугольник АОС - равнобедренный (ОО1 - высота, медиана и биссектриса), АО=ОС и КТ - его средняя линия (так как ВВ1=В1О - дано) => АК=ТС => четырехугольник АКТС - равнобедренная трапеция. Что и требовалось доказать.
2. Средняя линия трапеции - полусумма ее оснований. АС=2√2см (диагональ квадрата со стороной = 2см), а КТ=√2 (по Пифагору, так как треугольник КВ1Т - прямоугольный, равнобедренный, с катетами = 1). Тогда средняя линия трапеции равна 1,5*√2 см.
Объяснение:
CD⊥AD как касательная и радиус проведённый в точку касаний. AE=AD как радиусы одной окружности.
ΔACD ~ ΔCBD по двум углам (∠CAD=∠BCD и ∠ADC=90°=∠CDB), из подобия следует следующее отношение:
AD/CD=CD/DB
Откуда AD·DB = CD² = 144.
Пусть AD=x, тогда DB = AB-AD = 25-x.
x·(25-x) = 144;
x²-25x+144=0;
x(x-16)-9(x-16)=0;
(x-16)(x-9)=0 ⇒ x₁=16; x₂=9.
либо 16, либо 9.