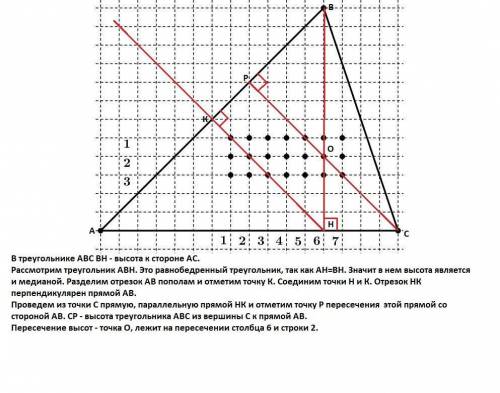
Пересечение 6 -2.
Объяснение:
В треугольнике АВС ВН - высота к стороне АС.
Рассмотрим треугольник АВН. Это равнобедренный треугольник, так как АН=ВН. Значит в нем высота является и медианой. Разделим отрезок АВ пополам и отметим точку К. Соединим точки Н и К. Отрезок НК перпендикулярен прямой АВ.
Проведем из точки С прямую, параллельную прямой НК и отметим точку Р пересечения этой прямой со стороной АВ. СР - высота треугольника АВС из вершины С к прямой АВ.
Пересечение высот - точка О, лежит на пересечении
столбца 6 и строки 2.
Украинский:
трикутник АВС, кут = 90, ВС - гіпотенуза, АН-висота на ВС, ВН = 28, СН = 7
ВН / АН = АН / НС. 28 / АН = АН / 7, АН в квадраті = 196, АН = 14
АС = корінь (АН в квадраті + НС в квадраті) = корінь (196 + 49) = корень245 = 7 х корень5
АВ = корінь (АН в квадраті + ВН в квадраті) = корінь (196 + 784) = корень980 =
= 14 х корень5
Площа = 1/2 х АС х АВ = 1/2 х 7 х корень5 х 14 х корень5 = 245
Русский:
треугольник АВс, уголА=90, ВС - гипотенуза, АН-высота на ВС, ВН=28, СН=7
ВН/АН=АН/НС. 28/АН=АН/7, АН в квадрате = 196, АН=14
АС = корень(АН в квадрате + НС в квадрате) = корень(196 + 49) =корень245 =7 х корень5
АВ = корень (АН в квадрате + ВН в квадрате) = корень(196 + 784) = корень980 =
=14 х корень5
Площадь = 1/2 х АС х АВ = 1/2 х 7 х корень5 х 14 х корень5 = 245
АВ=6, АА₁=5
прямоугольный ΔBFF₁:
BF=12 (BO*2, O -точка пересечения диагоналей основания призмы)
FF₁=5 (длина бокового ребра призмы)
по теорема Пифагора: (BF₁)²=12²+5²
BF₁=13
прямоугольный ΔAFF₁:
FF₁=5
AF по теореме косинусов из ΔAEF: AF²=6²+6²-2*6*6*cos120°
AF²=36+36-72*(-1/2), AF²=108
или по теореме Пифагора из прямоугольного ΔBAF:
AF²=BF²-AB², AF²=12²-6²,AF²=108
(AF₁)²=108+25
AF₁=√133