Ответ: 6 см
Объяснение: Угол между плоскостями — это угол между перпендикулярами, проведенными в этих плоскостях к одной точке на линии их пересечения.
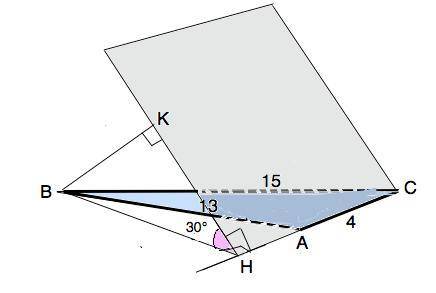
Линия пересечения - прямая СА, перпендикуляры к ней НВ и НК. Угол ВНК=30°(дано)
ВН - высота ∆ АВС к стороне АС. Площадь ∆ АВС по формуле Герона равна 24 см².
Из формулы площади треугольника высота ВН=2Ѕ:АС=48:4=12 (см).
Расстояние от точки до плоскости измеряется длиной перпендикуляра, опущенного из той точки на плоскость.
Из прямоугольного ∆ ВКН искомое расстояние ВК=ВН•sin30°=12•1/2=6 см
Объяснение:
О - точка пересечения диагоналей ВD и АС. ВО/OD=2/5. h=BC=4
1) Тр-ки ВОС и AOD подобны по трем соответственно равным углам (1 пара вертикальных и 2 пары накрест лежащих). Из подобия следует пропорциональность сходственных сторон: BC/AD=BO/OD; AD=BC*OD/BO=4*5/2=10.
2) Проведем две высоты ВN и СМ. Высоты разделят нижнее основание на отрезки;
NM=BC=4; AN=MD=(AD-NM)/2=3.
3) Тр-к ABN с катетами BN=4 и AN=3 - египетский. Значит, гипотенуза АВ=5. (А можно найти АВ по теореме Пифагора),
4) Р=2*АВ+BC+AD=10+4+10=24 см.
получим 360 - 215 -90 =55
55 это величина острого угла при нижнем основании