
.
Объяснение:
1) Так как ВС||АД, угол ВАС=углу АСД=35°, так как накрест лежащие углы. Угол САД=углу ВСА=30°, так как накрест лежащие углы.
Сумма углов треугольника равна 180°
Угол СДА=180°-(30°+35°)=115°
Угол АВС=180°-(35°+30°)=115°
2) Так как нам дан равнобедренный треугольник, то углы при основании равны.
Решим с уравнения:
Пусть углы при основании равны по х, тогда угол при вершине будет равен 4х.
Сумма углов треугольника равна 180°
Уравнение:
х+х+4х=180
6х=180
х=180:6
х=30
Углы при основании равны по 30°, тогда угол при вершине будет равен 180°-(30°+30°)=120°
3) Угол А=7х; угол В=3х; угол С=2х. Сумма углов треугольника равна 180°.
Решим с уравнения:
7х+3х+2х=180
12х=180
х=180:12
х=15
Угол А=7*15=105°
Угол В=3*15=45°
Угол С=2*15=30°
ответ: АС точкой пересечения диагоналей делится на АК=15 (см)
и КС=2•3=6 (см)
Объяснение:
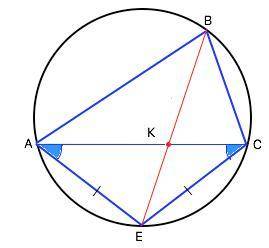
Треугольник АЕС - равнобедренный ( дано), => угол ЕАС=углу ЕСА. .
Вписанные углы СВЕ=ЕАС ( опираются на одну дугу - свойство вписанного угла)
Вписанные углы АВЕ=ЕСА ( опираются на одну дугу - свойство вписанного угла)
Но ∠ЕАС=∠ ЕСА, => ∠АВЕ=∠СВЕ, поэтому диагональ ВЕ - биссектриса угла АВС.
Биссектриса угла треугольника делит противоположную сторону в отношении, равном отношению двух прилежащих сторон. Пусть К - точка пересечения биссектрисой диагонали АС. Тогда АК:КС=АВ:ВС=5:2
АС=21=АК+КС
АС=5+2=7 частей
21:7=3 – длина одной части.
АК=5•3=15 (см)
КС=2•3=6 (см)
Угол 1 - 37°
Угол 2 - 143°
Объяснение:
При параллельных прямых односторонние углы в сумме будут давать 180°
Дадим самому маленькому числу переменную Х,в нашем случае углу 1:
х
Нам известно,что угол 2 на 106° больше угла 1,значит:
х+106
Составляем уравнение:
х+106°+х=180°
2х=180°-106°
2х=74°
х=37° (угол 1)
37°+106°=143° (угол 2)