Question

Знайти кути трикутника АВС, якщо А(3;-1), В(3;2),С(-1;-2)

Answer 1

Объяснение:

Угол А образован векторами АВ и АС. Находим их координаты, вычитая от координаты конечной точки координаты начальной.

AB = {3-3;2-(-1)} = {0;3}.

AC = {-1-3;-2-(-1)} = {-4;-1}.

cosA = (0*(-4) + 3*(-1)) / (√(0²+3²) * √((-4)²+(-1)²) = -3 / (3√17) = -1/√17 ≈-0.2425. ∠A = 104°. И про другие углы аналогично.

∠С=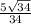$\frac{5\sqrt{34} }{34}$≈0,857  ∠С=31°

∠B=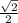$\frac{\sqrt{2} }{2}$≈0.707   ∠B=45°