
Т.к. высота равнобедренного треугольника перпендикулярна его основанию, а сама высота расположена на оси Ox, то само основание расположено на оси Oy.
По условиям задачи AC = BC = 5
Т.к. вершина треугольника находится в точке с координатами (4; 0), а основание высоты в точке (0; 0), то длину высоты определим по расстоянию между двумя этими точками:
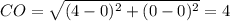
Из прямоугольного ΔAOC по теореме Пифагора найдем, что
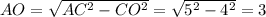
Т.к. высота равнобедренного треугольника проведенная к его основанию является одновременно медианой, то AO = BO.
Следовательно координаты точки A(3; 0), а точки B(-3; 0)
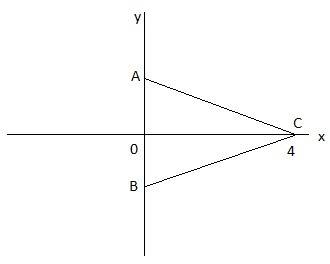
Объяснение:
Найдем углы треугольника из уравнения:
2х+3х+5х=180
10х=180
х=18
∠А=18*2=36° ∠В=18*3=54° ∠С=18*5=90°
ΔАВС - прямоугольный, т.к. содержит угол 90°
Самая длинная сторона - гипотенуза АВ, т.к. в треугольнике самая длинная сторона лежит против наибольшего угла.