
Объяснение: ЗАДАНИЕ 1
Если нужно найти угол В, то сумма острых углов прямоугольного треугольника составляет 90° поэтому угол В = 90-22=68°
ответ: угол В = 68°
ЗАДАНИЕ 2
Точно так же как и в 1- м задании: если угол В = 60°, то угол А=90-60=30°
Угол А=30°. Катет ВС лежит напротив этого угла и поэтому равен половине гипотенузы (свойство угла 30°). Значит гипотенуза АВ будет в 2 раза больше ВС: АВ=12×2=24; АВ=24
ОТВЕТ: АВ=24; угол А=30°
ЗАДАНИЕ 3
Так как катет ВС=160, а гипотенуза 320, значит катет ВС лежит напротив угла 30°, потому что он равен половине гипотенузы: 320÷2=160. Катет ВС лежит напротив угла А, значит угол А=30°, а угол В= 90-30=60°
ответ: угол А=30°, угол В=60°
Объяснение:
а) по теореме Пифагора найдём гипотенузу АВ: АВ²=АС²+ВС²
АВ=√(8²+6²)=√(64+36)=√100=10см
Зная, что центр описанной окружности около прямоугольного треугольника, является середина его гипотенузы. Поэтому R=AB÷2
R=10÷2=5см;
ответ: R=5см
б) катет, лежащий напротив угла 30° равен половине гипотенузы, поэтому гипотенуза АВ будет в 2 раза больше него: АВ=АС×2; АВ=18×2=36см;
Также R=AB÷2; R=36÷2=18.
ответ: R=18см
От себя добавлю что если вычислять по формуле, которая дана в задании, то результат получается другой. Например: следуя ей и используя данные задания "а", получится следующее: R=(a+b-c)÷2=(8+6-10)÷2=
=(14-10)÷2=4÷2=2. Совсем другой результат. Правило, что центр описанной окружности в прямоугольном треугольнике является середина гипотенузы, верно
ФОРМУЛА НА САМОМ ДЕЛЕ ТАКАЯ:
R=½×√(a²+b²), где " а" и "b"- катеты
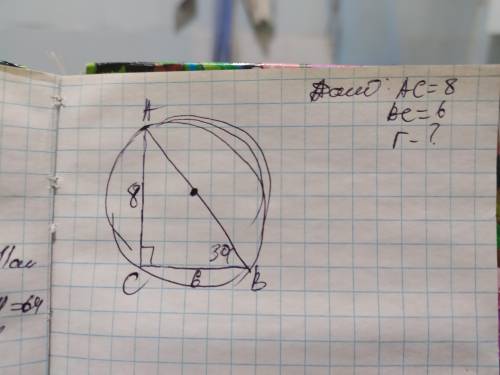
PF-7,5
Объяснение:
можно ЛУЧШИЙ ОТВЕТ?