№33 наклонная равна 20см. чему равна проекция этойнаклонной на плоскость, если наклонная составляет с плоскостью угол 45 градусов. №32 точка а отстоит от плоскости на расстоянии 26 см. найдите длину наклонной, которая
составляет с плоскостью угол 30 градусов . №31 дан куб abcda1b1c1d1, 1) выпишите грани, параллельные ребру aa1 2) выпишите рёбра, скрещивающиеся с ребром вс 3) выпишите рёбра, перпендикулярные плоскости (abb1) 4) выпишите
плоскости, перпендикулярные ребру ad. №30 радиусы оснований усечённого конуса равны здм и 7дм. образующая - 5дм. найдитеплощадь осевого сечения. №29 шар пересечён плоскостью на расстоянии зсм от центра. найдите
площадь сечения,если радиус шара равен 5см. №28 измерения прямоугольного параллелепипеда равны 8см, 12см, 18см. найдите ребро куба, объём которого равен объёму этого параллелепипеда. №27 дан куб abcda1b1c1d1, 1) найдите
прямую пересечения плоскостей (a1b1c1) и (bb1c1) 2) выпишите рёбра, параллельные грани a1b1c1d1 3) выпишите грани, параллельные ребру ad 4) выпишите рёбра, скрещивающиеся с ребром cc1 №26 радиус основания конуса 5см, его высота
12см. найдите площадь осевого сечения, длину образующей. №25 найдите боковую поверхность цилиндра с высотой 3 см, если осевое сечение цилиндраплоскостью - квадрат. №24 высота правильной четырёхугольной пирамиды
равна 1см, а сторона основания 4см.найдите боковое ребро. №23 боковое ребро наклонной призмы равно 20дм и наклонено к плоскости основания под углом 45 градусов найдите высоту призмы.
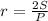 , где
, где 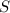 — площадь треугольника, а
— площадь треугольника, а  — его периметр.
— его периметр.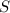 треугольника по формуле
треугольника по формуле 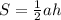 , где
, где 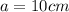 — основание, а
— основание, а  — высота, проведенная к основанию
— высота, проведенная к основанию  . Проведем к основанию
. Проведем к основанию  высоту
высоту  . Получился прямоугольный (
. Получился прямоугольный ( высота) треугольник с гипотенузой
высота) треугольник с гипотенузой  (
( — боковая стороны) и катетами
— боковая стороны) и катетами  и
и 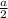 (так как треугольник равнобедренный, то высота, проведенная к основанию, является также медианой, то есть делит основание пополам, поэтому второй катет
(так как треугольник равнобедренный, то высота, проведенная к основанию, является также медианой, то есть делит основание пополам, поэтому второй катет 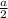 ). По теореме Пифагора найдем
). По теореме Пифагора найдем  :
:
 , найдем численное значение
, найдем численное значение  :
:

 :
: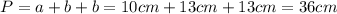

 см.
см.
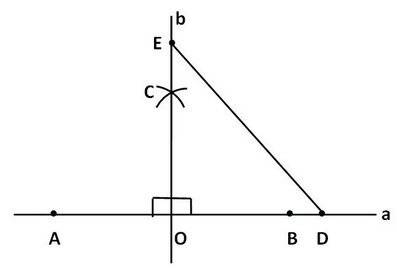
Наклонная равна 20см. чему равна проекция этой наклонной на плоскость, если
наклонная составляет с плоскостью угол 45 градусов.
L=20 cм, l = 20*cos45 = 20*√2/2 = 10√2 см
Точка А отстоит от плоскости на расстоянии 26 см. Найдите длину наклонной, которая составляет с плоскостью угол 30 градусов .
H=26 см, L=H/sin30 = 2H = 52 см
Дан куб ABCDA1B1C1D1,
1) Выпишите грани, параллельные ребру AA1 - не считая граней в которых лежит АА1, BB1C1C и СС1D1D
2) выпишите рёбра, скрещивающиеся с ребром ВС - А1В1, С1D1
3) выпишите рёбра, перпендикулярные плоскости (ABB1) - BC,B1C1,AD,A1D1
4) выпишите плоскости, перпендикулярные ребру AD - ABB1A1, CDD1C1
Радиусы оснований усечённого конуса равны Здм и 7дм. Образующая - 5дм. Найдите площадь осевого сечения.
Осевое сечение - трапеция с основаниями 6дм и 14 дм, и боковой стороной 5дм
S = h*(6+14)/2 = 10h.
Высоту найдем по теореме Пифагора h^2=5^2-((14-6)/2)^2 = 25-16 = 9, h=3 дм
S = 10*3 = 30 дм^2
Шар пересечён плоскостью на расстоянии Зсм от центра. Найдите площадь сечения, если радиус шара равен 5см.
Радиус сечения найдем из треугольника r^2 = R^2 - h^2 = 5^2-3^2 = 25-9 = 16
r = 4 см. S = пr^2 = 16п см^2
Измерения прямоугольного параллелепипеда равны 8см, 12см, 18см. найдите ребро куба, объём которого равен объёму этого параллелепипеда.
V = abc = 8*12*18 = 1728 см^3
Vкуба = а^3 = 1728, a = 4 ∛18 см