Медианы треугольника пересекаются в одной точке и делятся этой точкой в отношении 2:1, считая от вершины.
ВО:ОК=2:1
SO:ON=2:1
В равностороннем треугольнике медианы равны. Следовательно, равны и их сходственные отрезки.
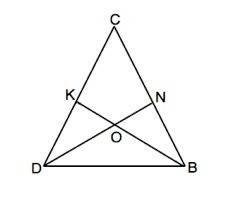
В ∆ DOK и ∆ BON равны две стороны и углы между ними при вершине О как вертикальные. Следовательно, эти треугольники равны по первому признаку.
--------
∆ DOK и ∆ BON равны и по 3-му признаку, т.к. у равных сторон равны и их половины.
А, поскольку медианы являются здесь и биссектрисами и высотами, то можно доказать их равенство и по второму признаку.
Решение: Рассмотрим треугольник ACH: Так как CH - высота,то этот треугольник прямоугольный. Следовательно CH - катет и мы находим его по теореме Пифагора: CH = √6^²-4^² = √36-16 = √20 = 2√5
Я предлагаю рассмотреть треугольник ABC и найти x через CB(не знаю можно ли так,как я решил,но я запишу)
AB=4+x
CB=√AB²-AC² = √(4-x)²-6² = √x²-10x-20
Разбираем квадратичное уравнение:
x²-10x-20=0
D= 100+4*20=180 √D= 6√5
x_{12} = 5+-3√5
x2 - не подходит,так как получается отрицательным,поэтому BH = 5+3√5.
ответ: 5+3√5