пусть ad> bc , тогда острые углы равные 75 и 15 гр лежат при оснований ad , положим что y,w середины сторон ab и cd соответственно , тогда yw средняя линия трапеции , значит ad+bc=2yw из условия мы знаем что yw равна либо 15 либо 7 , положим что ab и cd пересекаются в точке e , тогда aed=180-(75+15)=90 , положим также что z,x это середины сторон основании bc,ad соотвественно , пусть n точка пересечения yw и zx , тогда по замечательному свойству трапеции точки e,z,x лежат на одной прямой , учитывая что угол aed прямой , получаем что ax=ex=ad/2 , ez=bz=bc/2 , но так как ex=ez+zx откуда окончательно получаем две системы
{ad-bc=2*7
{ad+bc=2*15
или
{ad-bc=2*15
{ad+bc=2*7
подходит решение первой системы , так как они положительны , складывая получаем ad=22 , bc=8 , значит ответ bc=8.
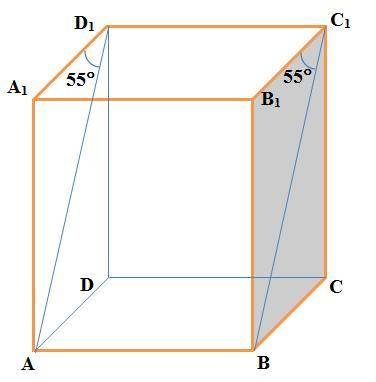
Угол между прямыми C₁B и AA₁ равен 35°
Объяснение:
Если одна из двух прямых лежит в некоторой плоскости, а другая прямая пересекает эту плоскость в точке, не лежащей на первой прямой, то эти прямые скрещивающиеся (не лежат в одной плоскости).
В задаче C₁B и AA₁ являются скрещивающимися прямыми (см. рисунок). Углом между двумя скрещивающимися прямыми называют угол между двумя пересекающимися прямыми, соответственно, параллельными данным скрещивающимся прямым.
В силу этого, так как C₁B || D₁A, то угол между прямыми C₁B и AA₁ равен углу между прямыми D₁A и AA₁, то есть ∠A₁AD₁. В треугольнике ΔAA₁D₁:
∠AD₁A₁+∠D₁A₁A+∠A₁AD₁=180°.
Тогда, так как ∠AA₁D₁=90° и ∠AD₁A₁=55°, то ∠A₁AD₁=180°–90°–55°=35°.
360 - 120 - 83 - 47 = 110 (градусов)
ответ: 110 градусов - четвёртый угол.