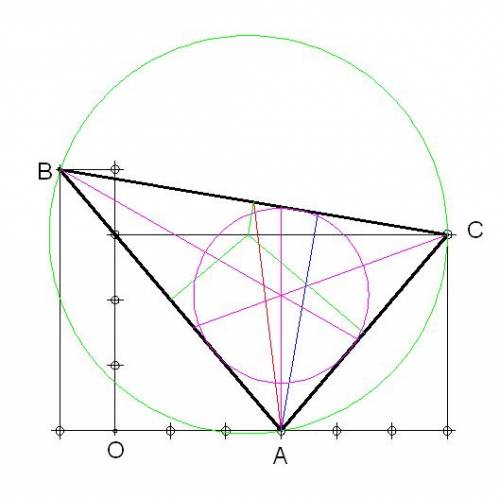
РАСЧЕТ ТРЕУГОЛЬНИКА
заданного координатами вершин:
Вершина 1: A(3; 0)
Вершина 2: B(-1; 4)
Вершина 3: C(6; 3)
ДЛИНЫ СТОРОН ТРЕУГОЛЬНИКА
Длина BС (a) = 7,07106781186548
Длина AС (b) = 4,24264068711928
Длина AB (c) = 5,65685424949238
ПЕРИМЕТР ТРЕУГОЛЬНИКА
Периметр = 16,9705627484771
ПЛОЩАДЬ ТРЕУГОЛЬНИКА
Площадь = 12
УГЛЫ ТРЕУГОЛЬНИКА
Угол BAC при 1 вершине A:
в радианах = 1,5707963267949
в градусах = 90
Угол ABC при 2 вершине B:
в радианах = 0,643501108793284
в градусах = 36,869897645844
Угол BCA при 3 вершине C:
в радианах = 0,927295218001612
в градусах = 53,130102354156
ЦЕНТР ТЯЖЕСТИ
Координаты Om(2,66666666666667; 2,33333333333333)
ВПИСАННАЯ ОКРУЖНОСТЬ
Центр Ci(3; 2)
Радиус = 1,4142135623731
ОПИСАННАЯ ОКРУЖНОСТЬ
Центр Co(2,5; 3,5)
Радиус = 3,53553390593274
МЕДИАНЫ ТРЕУГОЛЬНИКА
Медиана АM1 из вершины A:
Координаты M1(2,5; 3,5)
Длина AM1 = 3,53553390593274
ВЫСОТЫ ТРЕУГОЛЬНИКА
Высота AH1 из вершины A:
Координаты H1(3,48; 3,36)
Длина AH1 = 3,39411254969543
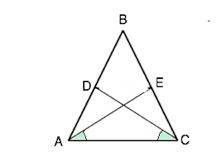
В равнобедренном треугольнике углы при основании равны.
Рассмотрим ∆ ВСD и ∆ BAЕ. ∠АВС- общий.
∠ВАЕ=∠ВАС-∠САЕ,
∠ВCD=∠ВСА-∠АСD. По условию ∠ЕАС=∠DCА, ⇒ ∠ВАЕ=∠ВСD
Треугольники ВАЕ и ВСD равны по стороне ( АВ=ВС по условию) и прилежащим к ней углам (ВАЕ=ВСD, угол В - общий). Следовательно, ВD=ВЕ. Доказано.
* * *
Вариант решения- доказать равенство треугольников АСD и АСЕ по общей стороне АС и двум прилежащим углам. Тогда при вычитании из равных сторон АВ и СВ равных отрезковостанутся равные BD и ВЕ
склрее всего это 25+3см и ×2