Отрезки пересекаются в их общей середине. Докажите, что .
Дано:.
Доказать: .
Доказательство:
Тогда, по первому признаку равенства треугольников, .
Тогда .
Поскольку эти углы являются накрест лежащими при прямых и секущей , то по первому признаку параллельности прямых , что и требовалось доказать.
Задача 1: отрезки и пересекаются в точке и делятся этой точкой пополам. Доказать параллельность и .Треугольники и равны по первому признаку равенства треугольников. и по условию. как вертикальные. Из равенства треугольников следует и равенство их соответствующих элементов. (накрест лежащие углы). Следовательно, прямые и параллельные. , что и требовалось доказать.
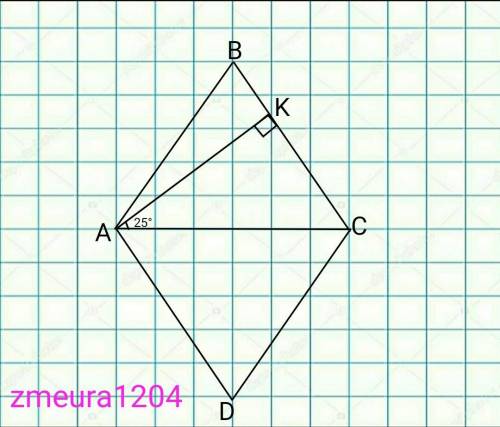
50°; 130°; 50°; 130°
Объяснение:
∆AKC- прямоугольный треугольник СК- высота.
Сумма острых углов в прямоугольном треугольнике равна 90°
<КАС+<КСА=90° →
<КСА=90°-<КАС=90°-25°=65°
Диагонали ромба являются биссектриссами углов.(свойство ромба)
<ВCD=2*KCA=2*65°=130°; (АС- биссектрисса угла <ВСD)
Сумма углов прилежащих к одной стороне ромба равна 180°
<ВСD+<ADC=180°, свойство ромба
<АDC=180°-<BCD=180°-130°=50°
Противоположные углы ромба равны.
<АDC=<ABC, свойство ромба
<ВСD=<BAD, свойство ромба
ОС - биссектриса,
угол 1 = 130⁰
угол 2 = 50⁰
АО=АС-?
угол АСО - ?
угол 3 = 180⁰ - угол 2 = 180⁰ - 50⁰ = 130⁰
угол 1 и угол 3 равны. при прямых АС и ОВ и сякущей АО - равны.
т.е. АС || ОВ , тогда
угол АОВ = 180⁰- угол 1 = 180⁰-130⁰=50⁰, как смежный.
С угол 1 , а угол 4 = угол 5 = 50⁰÷2=25⁰ угол АОС равнобедренный
ответ : АО=АС, угол АОС = 25⁰